
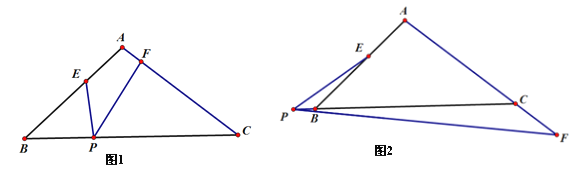
【题目】(1)如图1,△ABC中,∠BAC=100°,AB=AC,P为BC边上任意一点.若点E、F分别在AB、AC上,且∠EPF=40°,求证:△BPE∽△CFP;
(2)如图2,点P在边CB的延长线上,点E在边AB上,点F在边AC的延长线上,仍有∠EPF=40°,探索PB·PC与BE·CF有怎样的关系?并说明理由.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)由已知条件可得∠B=∠C=40°,由∠EPC=∠B+∠BEP,得∠EPF+∠FPC=∠B+∠BEP,而∠EPF=∠B=40°,从而可得∠FPC=∠BEP,从而得到△BPE∽△CFP;
(2)同(1)的道理类似,可得△BPE∽△CFP,从而可得![]() ,即PB·PC=BE·CF.
,即PB·PC=BE·CF.
试题解析:(1)∵△ABC中,∠BAC=100°,AB=AC,∴∠B=∠C=40°,∵∠EPC=∠B+∠BEP,∴∠EPF+∠FPC=∠B+∠BEP,又∵∠EPF=∠B=40°,∴∠FPC=∠BEP,∴△BPE∽△CFP;
相等,理由如下:
∵∠EBC=∠EPB+∠BEP,∴∠EPF=∠EPB+∠CPF,又∵∠EPF=∠B=40°,∴∠BEP=∠CPF,∵∠ABC=∠ACB,
∴∠EBP=∠PCF,∴△BPE∽△CFP,∴![]() ,∴PB·PC=BE·CF.
,∴PB·PC=BE·CF.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】如图,在三角形ABC中,已知AC⊥BC,CD⊥AB,∠1=∠2.对于下列五个结论:
①DE∥AC;
②∠1=∠B;
③∠3=∠A;
④∠3=∠EDB;
⑤∠2与∠3互补.
其中正确的有( )

A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时间,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:

(1)图中自变量是______,因变量是______;
(2)小明家到学校的路程是 米;
(3)小明在书店停留了 分钟;
(4)本次上学途中,小明一共行驶了 米,一共用了 分钟;
(5)我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(-4,n)、B(3,4)是一次函数y1=kx+b的图象与反比例函数![]() 的图象的两个交点,过点D(t,0)(0<t<3)作x轴的垂线,分别交双曲线
的图象的两个交点,过点D(t,0)(0<t<3)作x轴的垂线,分别交双曲线![]() 和直线y1=kx+b于P、Q两点
和直线y1=kx+b于P、Q两点
(1) 直接写出反比例函数和一次函数的解析式
(2) 当t为何值时,S△BPQ=![]() S△APQ
S△APQ
(3) 以PQ为边在直线PQ的右侧作正方形PQMN,试说明:边QM与双曲线![]() (x>0)始终有交点
(x>0)始终有交点

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D、E分别是等边三角形ABC的边BC、AC上的点,连接AD、BE交于点O,且△ABD≌△BCE.
(1)若AB=3,AE=2,则BD= ;
(2)若∠CBE=15°,则∠AOE= ;
(3)若∠BAD=a,猜想∠AOE的度数,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中∠C=90°,∠BAC=30°,AB=8,以2![]() 为边长的正方形DEFG的一边GD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是( )
为边长的正方形DEFG的一边GD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是( )

A. 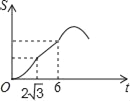 B.
B. 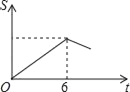 C.
C. 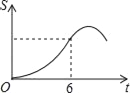 D.
D. 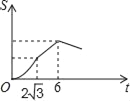
查看答案和解析>>
科目:初中数学 来源: 题型:
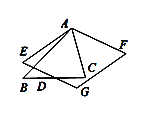
【题目】如图,△ABC中,∠BAC=60°,∠B=45°,AB=2,点D是BC上的一个动点,点D关于AB,AC的对称点分别是点E,F,四边形AEGF是平行四边形,则四边形AEGF面积的最小值是 ( )
A. 1B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
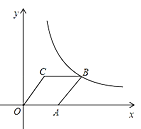
【题目】如图,菱形OABC的顶点C的坐标为(6,8).顶点A在x轴的正半轴上,反比例函数![]() 的图象经过顶B点.
的图象经过顶B点.
(1)求点A和B的坐标;
(2)求k值及直线AB对应的函数解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com