
【题目】超市销售某种儿童玩具,该玩具的进价为100元/件,市场管理部门规定,该种玩具每件利润不能超过进价的60%.现在超市的销售单价为140元,每天可售出50件,根据市场调查发现,如果销售单价每上涨2元,每天销售量会减少1件。设上涨后的销售单价为x元,每天售出y件.
(1)请写出y与x之间的函数表达式并写出x的取值范围;
(2)设超市每天销售这种玩具可获利w元,当x为多少元时w最大,最大为名少元?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,O为坐标原点,设点P的坐标为(x,y),当x<0时,点P的变换点P′的坐标为(y,﹣x);当x≥0时,点P的变换点P'的坐标为(﹣x,y).
(1)点A(1,2)的变换点A'的坐标是 ;
(2)点B(﹣2,3)的变换点B′在反比例函数y=![]() 的图象上,则k= ,∠BOB'的大小是 °;
的图象上,则k= ,∠BOB'的大小是 °;
(3)点P在抛物线y=﹣(x﹣2n)2+3上,点P的变换P′的坐标是(﹣4,﹣n),求n的值.
(4)点P在抛物线y=﹣x2﹣4x+1的图象上,以线段PP′为对角线作正方形PMP'N,设点P的横坐标为m,当正方形PMP′N的对角线垂直于x轴时,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
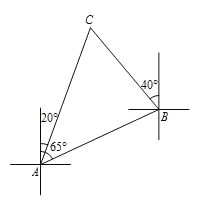
【题目】如图,一艘船由A港沿北偏东65°方向航行![]() km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向.
km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向.
求:(1)∠C的度数;
(2)A,C两港之间的距离为多少km.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(0,2)、B(a,a+2)、C(b,0)(a>0,b>0),若AB=![]() 且∠ACB最大时,b的值为( )
且∠ACB最大时,b的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴正半轴相交于A、B两点,与
轴正半轴相交于A、B两点,与![]() 轴相交于点C,对称轴为直线
轴相交于点C,对称轴为直线![]() 且OA=OC,则下列结论:①
且OA=OC,则下列结论:①![]() ②
②![]() ③
③![]() ④关于
④关于![]() 的方程
的方程![]() 有一个根为
有一个根为![]() 其中正确的结论个数有( )
其中正确的结论个数有( )
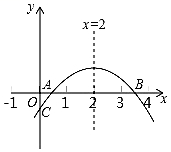
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给的平面直角坐标系中按要求作图并完成填空:
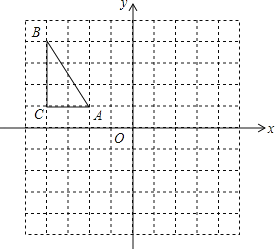
(1)作出△ABC关于原点O成中心对称的△A1B1C1,写出点A1的坐标_______.
(2)作出△A1B1C1绕点O逆时针旋转90°的△A2B2C2,写出线段C1C2的长度_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副扑克牌中点数为“2”、“3”、“4”、“6”的四张牌背面朝上洗匀,先从中抽出1张牌,记录下牌面点数为x,再从余下的3张牌中抽出1张牌,记录下牌面点数为y.设点P的坐标为(x,y).
(1)请用表格或树状图列出点P所有可能的坐标.
(2)求点P在抛物线y=x2+x上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
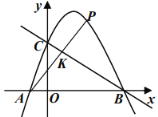
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() 为该二次函数在第一象限内的一点,连接
为该二次函数在第一象限内的一点,连接![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() 的最大值为__________.
的最大值为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com