
【题目】我国南宋时期杰出的数学家杨辉是钱塘人,如图是他在《详解九章算术》中记载的“杨辉三角”.此图揭示了(a+b)n(n为非负整数)的展开式的项数及各项系数的有关规律. 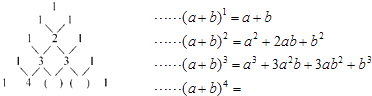
(1)请仔细观察,填出(a+b)4的展开式中所缺的系数.(a+b)4=a4+4a3b+a2b2+ab2+b4
(2)此规律还可以解决实际问题:假如今天是星期三,再过7天还是星期三,那么再过814天是星期 .
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校欲招聘一名数学教师,学校对甲、乙、丙三位候选人进行了三项能力测试,各项测试成绩满分均为100分,根据结果择优录用.三位候选人的各项测试成绩如下表所示:
测试项目 | |||
测试成绩/分 | |||
甲 | 乙 | 丙 | |
教学能力 | 85 | 73 | 73 |
科研能力 | 70 | 71 | 65 |
组织能力 | 64 | 72 | 84 |
(1)如果根据三项测试的平均成绩,谁将被录用,说明理由;
(2)根据实际需要,学校将教学、科研和组织三项能力测试得分按5∶3∶2的比例确定每人的成绩,谁将被录用,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数:
每人加工零件个数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数.
(2)假如生产部负责人把每位工人的月加工零件个数定为260,你认为这个定额是否合理?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市招聘教师,对应聘者分别进行教学能力、科研能力、组织能力三项测试,其中甲、乙两人的成绩如下表:(单位:分)

(1)根据实际需要,将教学能力、科研能力、组织能力三项测试得分按5∶3∶2的比确定最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
(2)按照(1)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值),并决定由高分到低分录用8人.甲、乙两人能否被录用?请说明理由.
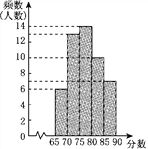
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1∥l2 , A是l1上一点,B是l2上一点,直线l3和直线l1 , l2交于点C和D,在直线CD上有一点P 
(1)如果P点在C、D之间运动时,问∠PAC、∠APB、∠PBD有怎样的数量关系?请说明理由.
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC、∠APB、∠PBD之间的关系又是如何?(请直接写出答案,不需要证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了丰富学生的第二课堂,对学生参与演讲、舞蹈、书法和摄影活动的兴趣情况进行调查,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中最感兴趣的一项),对调查结果进行统计后,绘制了如下两个统计图: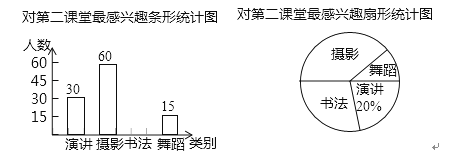
(1)此次调查抽取的学生人数m= 名,其中选择“书法”的学生占抽样人数的百分比n= ;
(2)若该校有3000名学生,请根据以上数据估计该校对“书法”最感兴趣的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com