
【题目】已知直线l1∥l2 , A是l1上一点,B是l2上一点,直线l3和直线l1 , l2交于点C和D,在直线CD上有一点P 
(1)如果P点在C、D之间运动时,问∠PAC、∠APB、∠PBD有怎样的数量关系?请说明理由.
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC、∠APB、∠PBD之间的关系又是如何?(请直接写出答案,不需要证明)
【答案】
(1)解:∠PAC+∠PBD=∠APB.
过点P作PE∥l1,如图1所示.
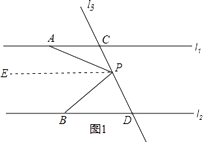
∵PE∥l1,l1∥l2,
∴PE∥l1∥l2,
∴∠PAC=∠APE,∠PBD=∠BPE,
∵∠APB=∠APE+∠BPE,
∴∠PAC+∠PBD=∠APB
(2)解:过点P作PE∥l1.
当点P在直线l1上方时,如图2所示.

∵PE∥l1,l1∥l2,
∴PE∥l1∥l2,
∴∠PAC=∠APE,∠PBD=∠BPE,
∵∠APB=∠BPE﹣∠APE,
∴∠PBD﹣∠PAC=∠APB.
当点P在直线l2下方时,如图3所示.
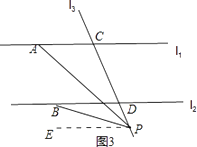
∵PE∥l1,l1∥l2,
∴PE∥l1∥l2,
∴∠PAC=∠APE,∠PBD=∠BPE,
∵∠APB=∠APE﹣∠BPE,
∴∠PAC﹣∠PBD=∠APB
【解析】(1)过点P作PE∥l1 , 由“平行与同一条直线的两直线平行”可得出PE∥l1∥l2 , 再由“两直线平行,内错角相等”得出∠PAC=∠APE、∠PBD=∠BPE,再根据角与角的关系即可得出结论.(2)按点P的两种情况分类讨论:过点P作PE∥l1 , 由“平行与同一条直线的两直线平行”可得出PE∥l1∥l2 , 再由“两直线平行,内错角相等”得出∠PAC=∠APE、∠PBD=∠BPE,再根据角与角的关系即可得出结论.
【考点精析】利用平行线的性质对题目进行判断即可得到答案,需要熟知两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8cm,BC=6cm,动点E从点A出发.以2cm/s的速度沿射线AD方向运动,以AE为底边,在AD的右侧作等腰直角角形AEF,当点F落在射线BC上时,点E停止运动,设△AEF与矩形ABCD重叠部分的面积为S,运动的时间为t(s).
(1)当t为何值时,点F落在射线BC上;
(2)当线段CD将△AEF的面积二等分时,求t的值;
(3)求S与t的函数关系式;
(4)当S=17时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为选派一名学生参加全市实践活动技能竞赛,A.B两位同学在学校实习基地现场进行加工直径为20mm的零件的测试,他俩各加工的10个零件的相关数据依次如下图表所示(单位:mm)
平均数 | 方差 | 完全符合要求个数 | |
A | 20 | 0.026 | 2 |
B | 20 | SB2 |
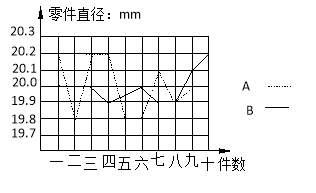
根据测试得到的有关数据,试解答下列问题:
⑴ 考虑平均数与完全符合要求的个数,你认为 的成绩好些;
⑵ 计算出SB2的大小,考虑平均数与方差,说明谁的成绩好些;
⑶ 考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况,你认为派谁去参赛较合适?说明你的理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,E为矩形ABCD边AD上一点,点P从点B沿折线BE﹣ED﹣DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.若P,Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2).已知y与t的函数图象如图2,则下列结论错误的是( )
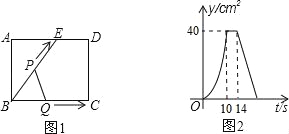
A.AE=6cm
B.sin∠EBC=![]()
C.当0<t≤10时,y=![]() t2
t2
D.当t=12s时,△PBQ是等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南宋时期杰出的数学家杨辉是钱塘人,如图是他在《详解九章算术》中记载的“杨辉三角”.此图揭示了(a+b)n(n为非负整数)的展开式的项数及各项系数的有关规律. 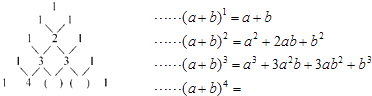
(1)请仔细观察,填出(a+b)4的展开式中所缺的系数.(a+b)4=a4+4a3b+a2b2+ab2+b4
(2)此规律还可以解决实际问题:假如今天是星期三,再过7天还是星期三,那么再过814天是星期 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次知识竞赛共20道题,每一题答对得10分,答错或不答都扣5分,小芳得分不低于80分.设她答对了x道题,则根据题意可列出不等式为( )
A. 10x﹣2(20﹣x)≥80 B. 10x﹣(20﹣x)>80
C. 10x﹣5(20﹣x)≥80 D. 10x﹣5(20﹣x)>80
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年3月3日到3月15日,两会在京矩形,雾霾防治问题受到国民的普遍关注,某报社决定以“对于雾霾,你最关注的话题是什么”为主题,通过街头随访和网络调查两种方式进行调查,根据调查所得数据绘制了表格.
最关注的话题 | 街头随访/人 | 网络调查/人 | 合计/人 |
雾霾是什么 | 120 | 200 | |
雾霾治理 | 40%a | 60%a | a |
雾霾中自我防护策略 | 600 | ||
其他话题 | 60 |
(1)参加本次街头随访和网络调查的总人数是多少人,a的值为多少;
(2)请你将以上表格中空白处补充完整;
(3)若在接受街头随访的人员中随机抽出一人,则抽到最关注“雾霾中自我防护策略”人员的概率是 多少? ;
查看答案和解析>>
科目:初中数学 来源: 题型:
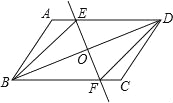
【题目】已知:如图,在ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)求证:△DOE≌△BOF;
(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com