
【题目】如图,在矩形ABCD中,AB=8cm,BC=6cm,动点E从点A出发.以2cm/s的速度沿射线AD方向运动,以AE为底边,在AD的右侧作等腰直角角形AEF,当点F落在射线BC上时,点E停止运动,设△AEF与矩形ABCD重叠部分的面积为S,运动的时间为t(s).
(1)当t为何值时,点F落在射线BC上;
(2)当线段CD将△AEF的面积二等分时,求t的值;
(3)求S与t的函数关系式;
(4)当S=17时,求t的值.

【答案】(1)8(2)6(3)S= (4)5
(4)5
【解析】
试题分析:(1)由矩形的性质和等腰直角三角形的性质得出FH=8cm,再由运动得出FH=t,即可;
(2)由等腰直角三角形的性质得出斜边上的高也是中线,根据三角形的中线把三角形AEF面积平分,判断出点F在CD上,即可;
(3)分三种情况先利用矩形和运动的特点显示出三角形高,底边和梯形的上下底,高,再利用三角形和梯形的面积公式求解;
(4)先判断出面积是17时,运动时间在3<t≤6内,再直接代入函数关系式中,即可.
试题解析:(1)如图1,

过点F作FH⊥AD于H,
在矩形ABCD中,AB=8cm,BC=6cm,∠BAD=90°,
∵点F落在射线BC上,
∴FH=8cm,
∴t=8s,
(2)如图2,

∵△AEF是等腰直角三角形,
∴AE边上的高线也是该边的中线,
∴点F在边CD上时,CD将△AEF的面积二等分,
∵FD是直角三角形的斜边的直线,
∴由运动知,FD=AD=6=t,
∴t=6s,
(3)当0<t≤3时,如图3,
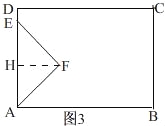
过点F作FH⊥AD,
由运动知,AE=2t,
∴FH=![]() AE=t,
AE=t,
∴S=![]() AE×FH=t2,
AE×FH=t2,
当3<t≤6时,如图4,

过点F作FH⊥AD,
由运动知,AE=2t,
∴DG=DE=2t﹣6,FH=t,DH=6﹣t,
∴S=![]() S△AEF+S梯形DHFG=
S△AEF+S梯形DHFG=![]() ×
×![]() AE×FH+
AE×FH+![]() (DG+FH)×DH=
(DG+FH)×DH=![]() ×
×![]() ×2t×t+
×2t×t+![]() (2t﹣6+t)×(6﹣t)=﹣t2+12t﹣18,
(2t﹣6+t)×(6﹣t)=﹣t2+12t﹣18,
当6<t≤8时,如图5,
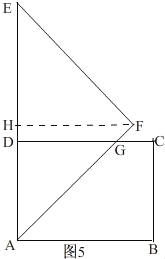
过点F作FH⊥AD,
∴DG=AD=6
∴S=![]() S△ADG=
S△ADG=![]() AD×GD=18;
AD×GD=18;
∴S=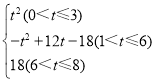 ,
,
(4)由函数关系式知,S=17的运动时间在3<t≤6中,
将S=17代入S=﹣t2+12t﹣18中,
∴﹣t2+12t﹣18=17,
∴t=7(舍)或t=5
∴当S=17时,t的值为5s.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
【题目】把下列各数按要求分类.
﹣4,200%,|﹣1|, ![]() ,﹣|﹣10.2|,2,﹣1.5,0,0.123,﹣25%
,﹣|﹣10.2|,2,﹣1.5,0,0.123,﹣25%
整数集合:{…},
分数集合:{…},
正整数集合:{…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
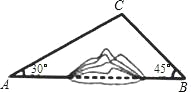
【题目】如图,A,B两地之间有一座山,汽车原来从A地到B地须经C地沿折线A﹣C﹣B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10km,∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果精确到0.1km)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫做△ABC的费马点.
(1)如果点P为锐角△ABC的费马点,且∠ABC=60°.
①求证:△ABP∽△BCP;
②若PA=3,PC=4,则PB= .
(2)已知锐角△ABC,分别以AB、AC为边向外作正△ABE和正△ACD,CE和BD 相交于P点.如图(2)
①求∠CPD的度数;
②求证:P点为△ABC的费马点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1∥l2 , A是l1上一点,B是l2上一点,直线l3和直线l1 , l2交于点C和D,在直线CD上有一点P 
(1)如果P点在C、D之间运动时,问∠PAC、∠APB、∠PBD有怎样的数量关系?请说明理由.
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC、∠APB、∠PBD之间的关系又是如何?(请直接写出答案,不需要证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com