
【题目】如图,在![]() 中,点
中,点![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,连接
,连接![]() .
.
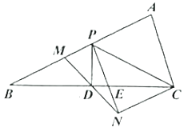
(1)求证:![]() ;
;
(2)连接![]() 交
交![]() 于点
于点![]() ,已知
,已知![]() ,求证:
,求证:![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
(1)由“ASA”可证△BMD≌△CND,可得BD=CD,由线段垂直平分线的性质可得PB=PC;
(2)如图,在PC上取点F,使CF=CN,连接EF,由“SAS”可证△CEN≌△CEF,可得EN=EF,∠CNP=∠CFE,由等腰三角形的判定可得EN=EF=PF,即可得结论.
证明:(1)∵CN∥AB,
∴∠B=∠BCN,∠BMD=∠CND,且BM=CN,
∴△BMD≌△CND(ASA)
∴BD=CD,且PD⊥BC,
∴PB=PC;
(2)如图,在PC上取点F,使CF=CN,连接EF,
∵PB=PC,
∴∠PCB=∠B,
∴∠PCB=∠NCB,且CF=CN,CE=CE,
∴△CEN≌△CEF(SAS),
∴EN=EF,∠CNP=∠CFE,
∵∠CFE=∠CPN+∠PEF,∠CNP=2∠CPN,
∴∠CPE=∠PEF,
∴PF=EF,
∴EN=EF=PF,
∵BP=PC,BM=CN=CF,
∴PM=PF=EN.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(-1,0),B(4,0)C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线![]() 交抛物线于点Q,交直线BD于点M.
交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)已知点F(0,![]() ),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=BC,∠B=90°,将△ABC沿BC方向平移,得到△A'CC',以C为位似中心,作△DEC与△ABC位似,位似比为1∶2,若F为CC'的中点,连接DF,A'F,则![]() 的值为_____.
的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
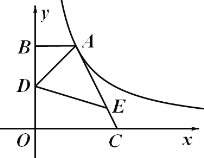
【题目】如图,点A在双曲线y=的第一象限的那一支上,AB垂直于x轴与点B,
点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE
的面积为3,则k的值为 ▲ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设菱形相邻两个内角的度数分别为![]() 和
和![]() ,将菱形的“接近度”定义为
,将菱形的“接近度”定义为![]() ,于是,
,于是,![]() 越小,菱形越接近于正方形.
越小,菱形越接近于正方形.
①若菱形的一个内角为![]() ,则该菱形的“接近度”等于 ;
,则该菱形的“接近度”等于 ;
②当菱形的“接近度”等于 时,菱形是正方形.

(2)设矩形相邻两条边长分别是![]() 和
和![]() (
(![]() ),将矩形的“接近度”定义为
),将矩形的“接近度”定义为![]() ,于是
,于是![]() 越小,矩形越接近于正方形.
越小,矩形越接近于正方形.
你认为这种说法是否合理?若不合理,给出矩形的“接近度”一个合理定义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体ABCD-A'B'C'D'是个无上底长方体容器,长AB=5cm,宽BC=3cm,高AA′=8cm,甜食点M在容器内侧,位于侧棱BB′的中点,一只蚂蚁从容器外部的A爬到点M处吃甜食,这只蚂蚁爬行的最短路径是( )cm
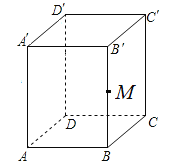
A.![]() B.13C.
B.13C.![]() D.14
D.14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长方形![]() 中,
中,![]() ,
,![]()
(1)如图1,将该长方形沿对角线![]() 折叠,求△BDE的周长?写出解题过程;
折叠,求△BDE的周长?写出解题过程;
(2)如图2,F是线段AB上的一个动点,在(1)的条件下,再将△AEF沿EF折叠,当A的对应点![]() 恰好落在BE上时,线段AF的值是 (直接写出答案)
恰好落在BE上时,线段AF的值是 (直接写出答案)
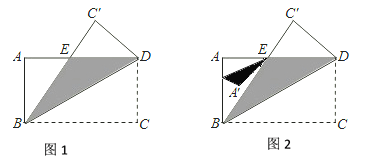
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品售后,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息,如表所示:
销售量n(件) | n=50﹣x |
销售单价m(元/件) | 当1≤x≤20时, |
当21≤x≤30时, |
(1)请计算第15天该商品单价为多少元/件?
(2)求网店销售该商品30天里所获利润y(元)关于x(天)的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC关于原点对称的△A1B1C1;
(2)四边形CBC1B1为 四边形;
(3)点P为平面内一点,若以点A、B、C、P为顶点的四边形为平行四边形,请直接写出所有满足条件的点P坐标.
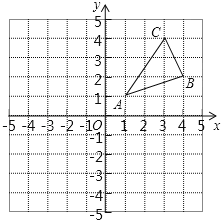
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com