
【题目】如图,已知抛物线经过点A(-1,0),B(4,0)C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线![]() 交抛物线于点Q,交直线BD于点M.
交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)已知点F(0,![]() ),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?

【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)m=﹣1或m=3时,四边形DMQF是平行四边形.
x+2;(2)m=﹣1或m=3时,四边形DMQF是平行四边形.
【解析】
(1)待定系数法求解可得;
(2)先利用待定系数法求出直线BD解析式为y=![]() x﹣2,则Q(m,﹣
x﹣2,则Q(m,﹣![]() m2+
m2+![]() m+2)、M(m,
m+2)、M(m,![]() m﹣2),由QM∥DF且四边形DMQF是平行四边形知QM=DF,据此列出关于m的方程,解之可得.
m﹣2),由QM∥DF且四边形DMQF是平行四边形知QM=DF,据此列出关于m的方程,解之可得.
(1)由抛物线过点A(﹣1,0)、B(4,0)可设解析式为y=a(x+1)(x﹣4),将点C(0,2)代入,得:﹣4a=2,解得:a=﹣![]() ,则抛物线解析式为y=﹣
,则抛物线解析式为y=﹣![]() (x+1)(x﹣4)=﹣
(x+1)(x﹣4)=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)由题意知点D坐标为(0,﹣2),设直线BD解析式为y=kx+b,将B(4,0)、D(0,﹣2)代入,得:![]() ,解得:
,解得: ,∴直线BD解析式为y=
,∴直线BD解析式为y=![]() x﹣2.
x﹣2.
∵QM⊥x轴,P(m,0),∴Q(m,﹣![]() m2+
m2+![]() m+2)、M(m,
m+2)、M(m,![]() m﹣2),则QM=﹣
m﹣2),则QM=﹣![]() m2+
m2+![]() m+2﹣(
m+2﹣(![]() m﹣2)=﹣
m﹣2)=﹣![]() m2+m+4.
m2+m+4.
∵F(0,![]() )、D(0,﹣2),∴DF=
)、D(0,﹣2),∴DF=![]() .
.
∵QM∥DF,∴当﹣![]() m2+m+4=
m2+m+4=![]() 时,四边形DMQF是平行四边形,解得:m=﹣1或m=3,即m=﹣1或m=3时,四边形DMQF是平行四边形.
时,四边形DMQF是平行四边形,解得:m=﹣1或m=3,即m=﹣1或m=3时,四边形DMQF是平行四边形.


科目:初中数学 来源: 题型:
【题目】中国北京已获得2022年第24届冬季奥林匹克运动会举办权,北京也将创造历史,成为第一个既举办过夏奥会又举办冬奥会的城市.张家口也成为本届冬奥会的协办城市,为此,中国设计了第一条采用我国自主研发的北斗卫星导航系统的智能化高速铁路——京张高铁,作为2022年北京冬奥会重要交通保障设施.已知北京至张家口铁路,铁路全长约180千米.按照设计,京张高铁列车的平均行驶速度是普通快车的1.5倍,用时比普通快车用时少了20分钟,求高铁列车的平均行驶速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解应用
待定系数法:设某一多项式的全部或部分系数为未知数、利用当两个多项式为恒等式时,同类项系数相等的原理确定这些系数,从而得到待求的值.
待定系数法可以应用到因式分解中,例如问题:因式分解![]() .
.
因为![]() 为三次多项式,若能因式分解,则可以分解成一个一次多项式和一个二次多项式的乘积.
为三次多项式,若能因式分解,则可以分解成一个一次多项式和一个二次多项式的乘积.
故我们可以猜想![]() 可以分解成
可以分解成![]() ,展开等式右边得:
,展开等式右边得:
![]() ,根据待定系数法原理,等式两边多项式的同类项的对应系数相等:
,根据待定系数法原理,等式两边多项式的同类项的对应系数相等:![]() ,
,![]() ,
,![]() 可以求出
可以求出![]() ,
,![]() .
.
所以![]() .
.
(1)若![]() 取任意值,等式
取任意值,等式![]() 恒成立,则
恒成立,则![]() ________;
________;
(2)已知多项式![]() 有因式
有因式![]() ,请用待定系数法求出该多项式的另一因式;
,请用待定系数法求出该多项式的另一因式;
(3)请判断多项式![]() 是否能分解成的两个均为整系数二次多项式的乘积,并说明理由.
是否能分解成的两个均为整系数二次多项式的乘积,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】百子回归图是由 1,2,3,…,100 无重复排列而成的正方形数表,它是一部数化的澳门简史,如:中央四 位“19 99 12 20”标示澳门回归日期,最后一行中间两 位“23 50”标示澳门面积,…,同时它也是十阶幻方, 其每行 10 个数之和、每列 10 个数之和、每条对角线10 个数之和均相等,则这个和为______.
百 子 回 归

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仙降是瑞安重要的制鞋基地,其生产的鞋子畅销世界各地,某制鞋企业欲将![]() 件产品运往
件产品运往![]() 三地销售,运往
三地销售,运往![]() 地的费用为18元/件,运往
地的费用为18元/件,运往![]() 地的费用为20元/件,运往
地的费用为20元/件,运往![]() 地的费用为17元/件,要求运往
地的费用为17元/件,要求运往![]() 地的件数与运往
地的件数与运往![]() 地的件数相同. 设安排
地的件数相同. 设安排![]() 件产品运往
件产品运往![]() 地.
地.
(1)若![]() ①运往
①运往![]() 地件数为 件(用含
地件数为 件(用含![]() 的代数式表示);②若总运费不超过1850元,则运往
的代数式表示);②若总运费不超过1850元,则运往![]() 地至少有多少件?
地至少有多少件?
(2)若总运费为1900元,则![]() 的最大值为 .(直接写出答案)
的最大值为 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)请画出△ABC关于直线m(直线m上各点的横坐标都为1)对称的图形.(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
(2)直接写出A′、B′、C′三点的坐标.
(3)平面内任一点P(x,y)关于直线m对称点的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
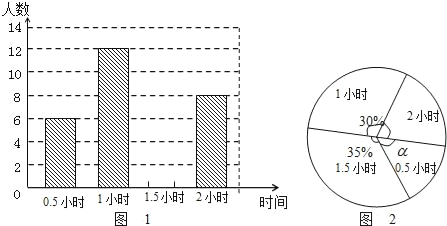
【题目】为了贯彻“减负增效”精神,掌握九年级600名学生每天的自主学习情况,某校学生会随机抽查了九年级的部分学生,并调查他们每天自主学习的时间.根据调查结果,制作了两幅不完整的统计图(图1,图2),请根据统计图中的信息回答下列问题:
(1)本次调查的学生人数是 人;
(2)图2中α是 度,并将图1条形统计图补充完整;
(3)请估算该校九年级学生自主学习时间不少于1.5小时有 人;
(4)老师想从学习效果较好的4位同学(分别记为A、B、C、D,其中A为小亮)随机选择两位进行学习经验交流,用列表法或树状图的方法求出选中小亮A的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com