
分析 把$\sqrt{{a}^{2}+a+1}$-$\sqrt{{a}^{2}-a+1}$,看作点(a,$\frac{\sqrt{3}}{2}$)到点(-$\frac{1}{2}$,0),($\frac{1}{2}$,0)的距离差.分三种情况①当a>0时,②当a=0时,③当a<0时分别求解即可.
解答 解:$\sqrt{{a}^{2}+a+1}$-$\sqrt{{a}^{2}-a+1}$=$\sqrt{[a-(-\frac{1}{2})]^{2}+(\frac{\sqrt{3}}{2}-0)^{2}}$-$\sqrt{(a-\frac{1}{2})^{2}+(\frac{\sqrt{3}}{2}-0)^{2}}$,可看作点(a,$\frac{\sqrt{3}}{2}$)到点(-$\frac{1}{2}$,0),($\frac{1}{2}$,0)的距离差.
①如图1,当a>0时,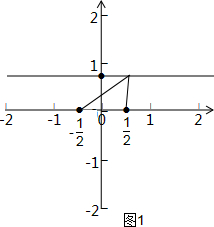
利用三角形三边关系可得0<$\sqrt{{a}^{2}+a+1}$-$\sqrt{{a}^{2}-a+1}$<1,
∵[x]表示不大于x的最大整数,
∴[$\sqrt{{a}^{2}+a+1}$-$\sqrt{{a}^{2}-a+1}$]=0,
②如图2,当a=0时,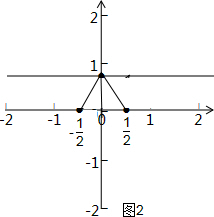
$\sqrt{{a}^{2}+a+1}$-$\sqrt{{a}^{2}-a+1}$=0,
∵[x]表示不大于x的最大整数,
∴[$\sqrt{{a}^{2}+a+1}$-$\sqrt{{a}^{2}-a+1}$]=0,
③如图3,当a<0时,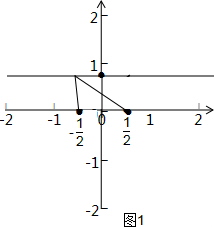
利用三角形三边关系可得-1<$\sqrt{{a}^{2}+a+1}$-$\sqrt{{a}^{2}-a+1}$<0,
∵[x]表示不大于x的最大整数,
∴[$\sqrt{{a}^{2}+a+1}$-$\sqrt{{a}^{2}-a+1}$]=-1,
综上所述:当a≥0时,[$\sqrt{{a}^{2}+a+1}$-$\sqrt{{a}^{2}-a+1}$]=0,
当a<0时,[$\sqrt{{a}^{2}+a+1}$-$\sqrt{{a}^{2}-a+1}$]=-1.
点评 本题主要考查了取整计算,解题的关键是利用数形结合,分类讨论的数学思想.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
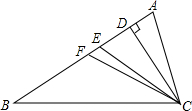 如图,CD、CE、CF分别是△ABC的高、角平分线、中线,则下列各式中错误的是( )
如图,CD、CE、CF分别是△ABC的高、角平分线、中线,则下列各式中错误的是( )| A. | BA=2BF | B. | ∠ACE=$\frac{1}{2}$∠ACB | C. | AE=BE | D. | CD⊥AB |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 南偏东60° | B. | 南偏西30° | C. | 南偏东30° | D. | 南偏西60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com