
分析 根据二次根式有意义的条件得到3-a>0,1-a>0,则a<1,于是根据二次根式的性质和二次根式的乘法法则得原式═$\frac{-(a-2)}{\sqrt{1-a}•\sqrt{3-a}}$•$\frac{\sqrt{3-a}}{a-2}$+$\frac{1}{\sqrt{1-a}}$,然后约分后合并即可.
解答 解:∵3-a>0,1-a>0,
∴a<1
∴原式=$\frac{|a-2|}{\sqrt{(1-a)(3-a)}}$•$\frac{\sqrt{3-a}}{a-2}$+$\frac{1}{\sqrt{1-a}}$
=$\frac{-(a-2)}{\sqrt{1-a}•\sqrt{3-a}}$•$\frac{\sqrt{3-a}}{a-2}$+$\frac{1}{\sqrt{1-a}}$
=-$\frac{1}{\sqrt{1-a}}$+$\frac{1}{\sqrt{1-a}}$
=0.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了二次根式有意义的条件.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:填空题
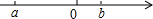 a,b在数轴上如图,则:
a,b在数轴上如图,则:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com