
【题目】已知抛物线![]() 经过点A(1,0)和B(0,3),其顶点为D.
经过点A(1,0)和B(0,3),其顶点为D.
(1)求此抛物线的表达式;
(2)求△ABD的面积;
(3)设P为该抛物线上一点,且位于抛物线对称轴右侧,作PH⊥对称轴,垂足为H,若△DPH与△AOB相似,求点P的坐标.
【答案】(1)![]() ;(2)点P的坐标为(5,8),
;(2)点P的坐标为(5,8),![]() .
.
【解析】试题分析:(1)把A、B的坐标代入抛物线的解析式,解方程组即可;
(2)作DT⊥y轴于点T,由S△ABD= S△BTD -S△AOB-SOTDA计算即可;
(3)令P(p,p2-4p+3) (p>2).由△DPH与△AOB相似,易知∠AOB=∠PHD=90°,然后分两种情况讨论即可.
试题解析:解:(1)由题意得: ![]() ,
,
解得: ![]() ,
,
所以抛物线的表达式为![]() .
.
(2)由(1)得D(2,﹣1),作DT⊥y轴于点T,
则△ABD的面积=![]() .
.
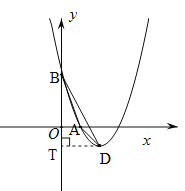
(3)令P![]() .由△DPH与△AOB相似,易知∠AOB=∠PHD=90°,所以
.由△DPH与△AOB相似,易知∠AOB=∠PHD=90°,所以![]() 或
或![]() ,解得:
,解得: ![]() 或
或![]() ,所以点P的坐标为(5,8),
,所以点P的坐标为(5,8),![]() .
.


科目:初中数学 来源: 题型:
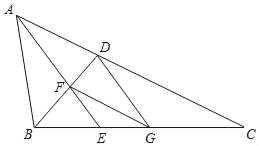
【题目】如图,已知在△ABC中,∠BAC=2∠C,∠BAC的平分线AE与∠ABC的平分线BD相交于点F,FG∥AC,联结DG.
(1)求证:BFBC=ABBD;
(2)求证:四边形ADGF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1) (-8)-47+18-(-27)
(2)-![]() ;
;
(3)12-(-18)+(-7)-15;
(4)4.7-(-8.9)-7.5+(-6);
(5)(4![]() ;
;
(6)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.
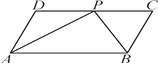
(1)求∠APB的度数;
(2)如果AD=5 cm,AP=8 cm,求△APB的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
(1)填空: a= ,b= ,c= ;
(2)先化简,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)]+4abc.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017浙江省湖州市)如图,已知∠AOB=30°,在射线OA上取点O1,以O1为圆心的圆与OB相切;在射线O1A上取点O2,以O2为圆心,O2O1为半径的圆与OB相切;在射线O2A上取点O3,以O3为圆心,O3O2为半径的圆与OB相切;…;在射线O9A上取点O10,以O10为圆心,O10O9为半径的圆与OB相切.若⊙O1的半径为1,则⊙O10的半径长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图①,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,点P在该抛物线上(P点与A、B两点不重合).如果△ABP的三边满足AP2+BP2=AB2,则称点P为抛物线y=ax2+bx+c(a≠0)的勾股点.
(1)直接写出抛物线y=-x2+1的勾股点的坐标.
(2)如图②,已知抛物线y=ax2+bx(a≠0)与x轴交于A,B两点,点P(1, ![]() )是抛物线的勾股点,求抛物线的函数表达式.
)是抛物线的勾股点,求抛物线的函数表达式.
(3)在(2)的条件下,点Q在抛物线上,求满足条件S△ABQ=S△ABP的Q点(异于点P)的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区的三个景点A、B、C在同一线路上.甲、乙两名游客从景点A出发,甲步行到景点C;乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C,甲、乙两人同时到达景点C.甲、乙两人距景点A的路程y(米)与甲出发的时间x(分)之间的函数图象如图所示.
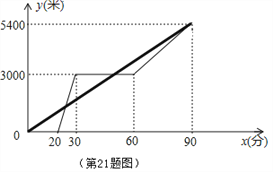
(1)乙步行的速度为_ __米/分.
(2)求乙乘景区观光车时y与x之间的函数关系式.
(3)甲出发多长时间与乙第一次相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 、
、![]() 、
、![]() 是数轴上三点,点
是数轴上三点,点![]() 表示的数为
表示的数为![]() ,
, ![]() ,
, ![]() .
.
(![]() )写出数轴上点
)写出数轴上点![]() 、
、![]() 表示的数:__________,__________.
表示的数:__________,__________.
(![]() )动点
)动点![]() ,
, ![]() 同时从
同时从![]() ,
, ![]() 出发,点
出发,点![]() 以每秒
以每秒![]() 个单位长度的速度沿数轴向右匀速运动,点
个单位长度的速度沿数轴向右匀速运动,点![]() 以
以![]() 个单位长度的速度沿数向左匀速运动,设运动时间为
个单位长度的速度沿数向左匀速运动,设运动时间为![]() 秒.
秒.
①求数轴上点![]() ,
, ![]() 表示的数(用含
表示的数(用含![]() 的式子表示);
的式子表示);
②![]() 为何值时,点
为何值时,点![]() ,
, ![]() 相距
相距![]() 个单位长度.
个单位长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com