
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 、
、![]() 是圆上的两点,且
是圆上的两点,且![]() 平分
平分![]() ,过点
,过点![]() 作
作![]() 延长线的垂线
延长线的垂线![]() ,垂足为
,垂足为![]() .若
.若![]() 的半径为
的半径为![]() ,
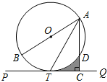
,![]() ,则图中阴影部分的面积是________.
,则图中阴影部分的面积是________.
【答案】![]()
【解析】
连接OT、OD、过O作OM⊥AD于M,得到矩形OMCT,求出OM,求出∠OAM,求出∠AOT,求出OT∥AC,得出PC是圆的切线,得出等边三角形AOD,求出∠AOD,求出∠DOT,求出∠DTC=∠CAT=30°,求出DC,求出梯形OTCD的面积和扇形OTD的面积.相减即可求出答案.
解:连接OT、OD、DT,过O作OM⊥AD于M,

∵OA=OT,AT平分∠BAC,
∴∠OTA=∠OAT,∠BAT=∠CAT,
∴∠OTA=∠CAT,
∴OT∥AC,
∵PC⊥AC,
∴OT⊥PC,
∵OT为半径,
∴PC是⊙O的切线,
∵OM⊥AC,AC⊥PC,OT⊥PC,
∴∠OMC=∠MCT=∠OTC=90°,
∴四边形OMCT是矩形,
∴OM=TC=![]() ,
,
∵OA=2,
∴sin∠OAM=![]() ,
,
∴∠OAM=60°,
∴∠AOM=30°
∵AC∥OT,
∴∠AOT=180°-∠OAM=120°,
∵∠OAM=60°,OA=OD,
∴△OAD是等边三角形,
∴∠AOD=60°,
∴∠TOD=120°-60°=60°,
∵PC切⊙O于T,
∴∠DTC=∠CAT=![]() ∠BAC=30°,
∠BAC=30°,
∴tan30°=![]() =
=![]() ,
,
∴DC=1,
∴阴影部分的面积是S梯形OTCD-S扇形OTD=![]() ×(2+1)×
×(2+1)×![]() -
-![]() =
=![]() .
.
故答案为:![]() .
.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
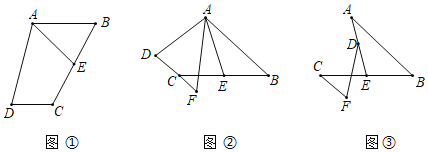
【题目】(1)问题探究:如图①,在四边形ABCD中,AB∥CD,E是BC的中点,AE是∠BAD的平分线,则线段AB,AD,DC之间的等量关系为 ;
(2)方法迁移:如图②,在四边形ABCD中,AB∥CD,AF与DC的延长线交于点F,E是BC的中点,AE是∠BAF的平分线,试探究线段AB,AF,CF之间的等量关系,并证明你的结论;
(3)联想拓展:如图③,AB∥CF,E是BC的中点,点D在线段AE上,∠EDF=∠BAE,试探究线段AB,DF,CF之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象与x轴交于点A(-1, 0),与y轴交于点C(0,-5),且经过点D(3,-8).
的图象与x轴交于点A(-1, 0),与y轴交于点C(0,-5),且经过点D(3,-8).
(1)求此二次函数的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在原点处,并写出平移后抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
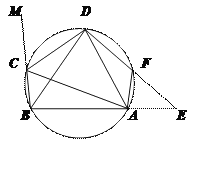
【题目】在圆内接四边形ABCD中,CD为∠BCA外角的平分线,F为弧AD上一点,BC=AF,延长DF与BA的延长线交于E.
⑴求证△ABD为等腰三角形.
⑵求证ACAF=DFFE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列正确的选项是( )
A.命题“同旁内角互补”是真命题
B.“作线段AC”这句话是命题
C.“对顶角相等”是定义
D.说明命题“若x>y,则a2x>a2y”是假命题,只能举反例a=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于A(2,m),B(-3,﹣2)两点.
的图象交于A(2,m),B(-3,﹣2)两点.
(1)求m的值;
(2)根据所给条件,请直接写出不等式k1x+b>![]() 的解集;
的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=![]() 图象上的两点, 且y1>y2,求实数p的取值范围.
图象上的两点, 且y1>y2,求实数p的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长都为1,△ABC的顶点都在格点上(网格线的交点).
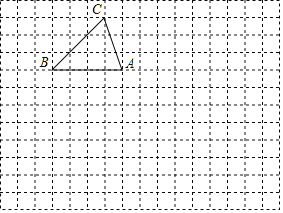
(1)请在如图所示的网格平面内建立适当的平面直角坐标系,使点A坐标为(﹣1,2),点B的坐标为(﹣5,2);(画出直角坐标系)
(2)点C的坐标为( , )(直接写出结果)
(3)把△ABC先向下平移6个单位后得到对应的△A1B1C1,再将△A1B1C1沿y轴翻折至△A2B2C2;
①请在坐标系中画出△A2B2C2;
②若点P(m,n)是△ABC边上任意一点,P2是△A2B2C2边上与P对应的点,写出点P2的坐标为( , );(直接写出结果)
③试在y轴上找一点Q,使得点Q到A2,C2两点的距离之和最小,此时,QA2+QC2的长度之和最小值为 .(在图中画出点Q的位置,并直接写出最小值答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校九年级学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题:
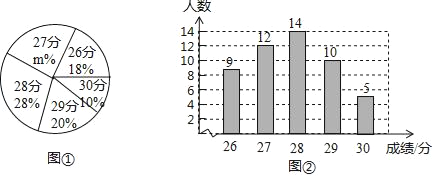
(1)本次随机抽样调查的学生人数为______,图①中的m的值为______;
(2)求本次抽样调查获取的样本数据的众数、中位数和平均数;
(3)若该校九年级共有学生300人,如果体育成绩达28分以上(含28分)为优秀,请估计该校九年级学生体育成绩达到优秀的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com