
分析 现将被除式分母因式分解、括号内通分化为同分母分式相加,括号内分式相加将除法转化为乘法,约分即可,最后将a的值代入计算.
解答 解:原式=$\frac{a+1}{(a-1)^{2}}÷(\frac{a-1}{a-1}+\frac{2}{a-1})$
=$\frac{a+1}{(a-1)^{2}}•\frac{a-1}{a+1}$
=$\frac{1}{a-1}$,
当a=$\sqrt{2}$+1时,
原式=$\frac{1}{\sqrt{2}+1-1}$
=$\frac{1}{\sqrt{2}}$
=$\frac{\sqrt{2}}{2}$.
点评 本题主要考查分式的化简求值能力,需要对通分、分解因式、约分等知识点熟练掌握,分式的混合运算需特别注意运算顺序及符号的处理.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
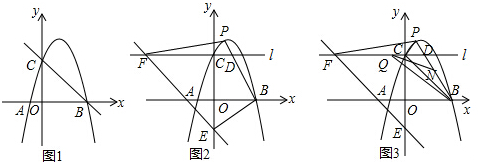
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2•a3=a6 | B. | (a3)2=a9 | C. | (-$\frac{1}{2}$)-1=-2 | D. | (sin30°-π)0=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解不等式组$\left\{\begin{array}{l}{\frac{1}{2}x>1}&{①}\\{1-x≥-3}&{②}\end{array}\right.$
解不等式组$\left\{\begin{array}{l}{\frac{1}{2}x>1}&{①}\\{1-x≥-3}&{②}\end{array}\right.$查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 尺码 | 22 | 22.5 | 23 | 23.5 | 24 | 24.5 | 25 |
| 数量(双) | 3 | 5 | 10 | 15 | 8 | 3 | 2 |
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2500}{x}$=$\frac{3000}{x-50}$ | B. | $\frac{2500}{x}$=$\frac{3000}{x+50}$ | C. | $\frac{2500}{x-50}$=$\frac{3000}{x}$ | D. | $\frac{2500}{x+50}$=$\frac{3000}{x}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com