
 如图,在圆心角为90°的扇形OAB中,半径OA=4,C为$\widehat{AB}$的中点,D、E分别为OA,OB的中点,则图中阴影部分的面积为2π+2$\sqrt{2}$-2.
如图,在圆心角为90°的扇形OAB中,半径OA=4,C为$\widehat{AB}$的中点,D、E分别为OA,OB的中点,则图中阴影部分的面积为2π+2$\sqrt{2}$-2. 分析 连接OC、EC,由△OCD≌△OCE、OC⊥DE可得DE=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,分别求出S扇形OBC、S△OCD、S△ODE面积,根据S扇形OBC+S△OCD-S△ODE=S阴影部分可得.
解答 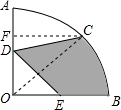 解:连结OC,过C点作CF⊥OA于F,
解:连结OC,过C点作CF⊥OA于F,
∵半径OA=4,C为$\widehat{AB}$的中点,D、E分别是OA、OB的中点,
∴OD=OE=2,OC=4,∠AOC=45°,
∴CF=2$\sqrt{2}$,
∴空白图形ACD的面积=扇形OAC的面积-三角形OCD的面积
=$\frac{45π×{4}^{2}}{360}$-$\frac{1}{2}$×2×2$\sqrt{2}$
=2π-2$\sqrt{2}$,
三角形ODE的面积=$\frac{1}{2}$OD×OE=2,
∴图中阴影部分的面积=扇形OAB的面积-空白图形ACD的面积-三角形ODE的面积
=$\frac{90π×{4}^{2}}{360}$-(2π-2$\sqrt{2}$)-2
=2π+2$\sqrt{2}$-2.
故答案为:2π+2$\sqrt{2}$-2.
点评 考查了扇形面积的计算,本题难点是得到空白图形ACD的面积,关键是理解图中阴影部分的面积=扇形OAB的面积-空白图形ACD的面积-三角形ODE的面积.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲 | 乙 | |
| 进价(元/件) | 40 | 60 |
| 售价(元/件) | 60 | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com