
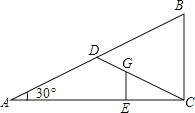
【题目】如图,在Rt△ABC中,∠A=30°,点D是斜边AB的中点,点G是Rt△ABC的重心,GE⊥AC于点E.若BC=6cm,则GE=__cm.
科目:初中数学 来源: 题型:
【题目】某校九年级数学兴趣小组在探究相似多边形问题时,他们提出了下面两个观点:
观点一:将外面大三角形按图1的方式向内缩小,得到新三角形,它们对应的边间距都为![]() ,则新三角形与原三角形相似.
,则新三角形与原三角形相似.
观点二:将邻边为![]() 和
和![]() 的矩形按图2方式向内缩小,得到新的矩形,它们对应的边间距都为
的矩形按图2方式向内缩小,得到新的矩形,它们对应的边间距都为![]() ,则新矩形与原矩形相似.
,则新矩形与原矩形相似.
请回答下列问题:

(1)你认为上述两个观点是否正确?请说明理由.
(2)如图3,已知![]() ,
,![]() ,
,![]() ,
,![]() ,将
,将![]() 按图3的方式向外扩张,得到
按图3的方式向外扩张,得到![]() ,它们对应的边间距都为
,它们对应的边间距都为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平行四边形ABCD,连接AF,CE、AF平分![]() 交BC于点F,CE平分
交BC于点F,CE平分![]() 交AD于点E.
交AD于点E.
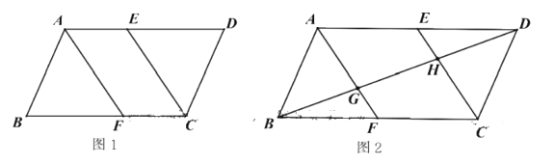
(1)如图1,求证:四边形AFCE为平行四边形;
(2)如图2,连接BD,分别交AF、CE于G、H,若![]() ,在不添加其他辅助线的情况下,直接找出图中面积为平行四边形ABCD面积的
,在不添加其他辅助线的情况下,直接找出图中面积为平行四边形ABCD面积的![]() 的三角形或四边形.
的三角形或四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加学校举行的传统文化知识竞赛,某班进行了四次模拟训练,将成绩优秀的人数和优秀率绘制成如下两个不完整的统计图:

![]()
(1)该班总人数是 ;
(2)根据计算,请你补全两个统计图;
(3)观察补全后的统计图,写出一条你发现的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在Rt△ABC中,∠C=90°,AD是∠BAC的角平分线,以AB上一点O为圆心,AD为弦作⊙O.
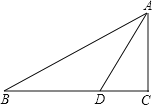
(1)用直尺和圆规在图中作出⊙O(不写作法,保留作图痕迹),判断直线BC与⊙O的位置关系,并说明理由;(友情提醒:必须作在答题卷上哦!)
(2)若AC=3,BC=4,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一块含30°(即∠CAB=30°)角的三角板和一个量角器拼在一起,三角板斜边AB与量角器所在圆的直径MN恰好重合,其量角器最外缘的读数是从N点开始(即N点的读数为0°),现有射线CP绕点C从CA的位置开始按顺时针方向以每秒2度的速度旋转到CB位置,在旋转过程中,射线CP与量角器的半圆弧交于E.

(1)当旋转7.5秒时,连接BE,试说明:BE=CE;
(2)填空:①当射线CP经过△ABC的外心时,点E处的读数是 .
②当射线CP经过△ABC的内心时,点E处的读数是 ;
③设旋转x秒后,E点出的读数为y度,则y与x的函数式是y= .
查看答案和解析>>
科目:初中数学 来源: 题型:
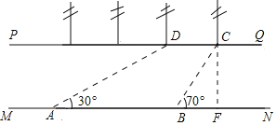
【题目】如图,河流两岸PQ,MN互相平行,C、D是河岸PQ上间隔50m的两个电线杆,某人在河岸MN上的A处测得∠DAB=30°,然后沿河岸走了100m到达B处,测得∠CBF=70°,求河流的宽度(结果精确到个位,![]() =1.73,sin70°=0.94,cos70°=0.34,tan70°=2.75)
=1.73,sin70°=0.94,cos70°=0.34,tan70°=2.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
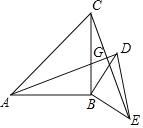
【题目】如图,△ABC和△BED都是等腰直角三角形,∠ABC=∠DBE=90°,AD,CE相交于点G
(1)求证:△ABD≌△CBE;
(2)求证:AD⊥CE;
(3)连接AE,CD,若AE=![]() CD=5,求△ABC和△BED的面积之和.
CD=5,求△ABC和△BED的面积之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com