
【题目】(1)计算(﹣2)3+![]() +|1﹣
+|1﹣![]() |0﹣4sin60°
|0﹣4sin60°
(2)化简代数式![]() ,再从﹣2≤a≤2中选一个恰当的整数作为a的值,代入求值.
,再从﹣2≤a≤2中选一个恰当的整数作为a的值,代入求值.
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
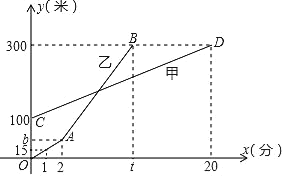
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,平面内互相垂直且有公共原点的两条数轴构成平面直角坐标系,如果两条数轴不垂直,而是相交成任意的角ω(0°<ω<180°且ω≠90°),那么这两条数轴构成的是平面斜坐标系,两条数轴称为斜坐标系的坐标轴,公共原点称为斜坐标系的原点,如图1,经过平面内一点P作坐标轴的平行线PM和PN,分别交x轴和y轴于点M,N.点M、N在x轴和y轴上所对应的数分别叫做P点的x坐标和y坐标,有序实数对(x,y)称为点P的斜坐标,记为P(x,y)

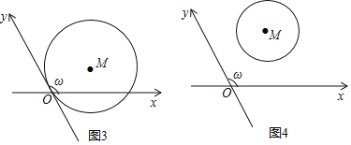
(1)如图2,ω=45°,矩形OABC中的一边OA在x轴上,BC与y轴交于点D,
OA=2,OC=1.
①点A、B、C在此斜坐标系内的坐标分别为A ,B ,C .
②设点P(x,y)在经过O、B两点的直线上,则y与x之间满足的关系为 .
③设点Q(x,y)在经过A、D两点的直线上,则y与x之间满足的关系为 .
(2)若ω=120°,O为坐标原点.
①如图3,圆M与y轴相切原点O,被x轴截得的弦长OA=2![]() ,求圆M的半径及圆心M的斜坐标.
,求圆M的半径及圆心M的斜坐标.
②如图4,圆M的圆心斜坐标为M(2![]() ,2
,2![]() ),若圆上恰有两个点到y轴的距离为1,则圆M的半径r的取值范围是 .
),若圆上恰有两个点到y轴的距离为1,则圆M的半径r的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,分别以顶点A、B为圆心,大于![]() AB为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线MN,与AB交于点O,以O为圆心,OA为半径作圆,⊙O恰好经过点C.下列结论中,错误的是( )
AB为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线MN,与AB交于点O,以O为圆心,OA为半径作圆,⊙O恰好经过点C.下列结论中,错误的是( )
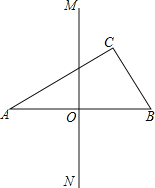
A.AB是⊙O的直径B.∠ACB=90°
C.△ABC是⊙O内接三角形D.O是△ABC的内心
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y= -x+3与x轴,y轴分别相交于点B、C,经过B、C两点的抛物线![]() 与x轴的另一交点为A,顶点为P,且对称轴为直线x=2.
与x轴的另一交点为A,顶点为P,且对称轴为直线x=2.
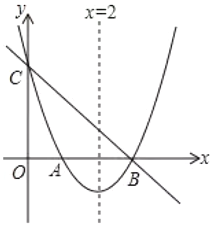
(1)求A点的坐标;
(2)求该抛物线的函数表达式;
(3)连结AC.请问在x轴上是否存在点Q,使得以点P、B、Q为顶点的三角形与△ABC 相似,若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 内接于⊙
内接于⊙![]() ,直径
,直径![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() .过点
.过点![]() 作⊙
作⊙![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() .
.
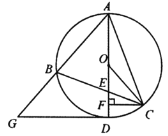
(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,连接![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,若
,若![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
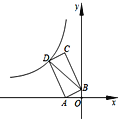
【题目】如图,点A(-2,0),B(0,1),以线段AB为边在第二象限作矩形ABCD,双曲线![]() (k<0)经过点D,连接BD,若四边形OADB的面积为6,则k的值是_____.
(k<0)经过点D,连接BD,若四边形OADB的面积为6,则k的值是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com