
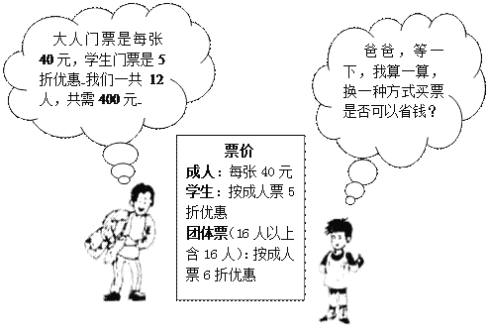
【题目】暑假期间,七(2)班的张明、王强等同学随家长一同到某公园游玩,下面是购买门票时,张明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
⑴ 张明他们一共去了几个成人,几个学生?
⑵ 请你帮助张明算一算,用哪种方式购票(团体购票还是非团体购票)更省钱?
说明理由.
⑶ 正要购票时,张明发现七(3)班的张小毛等15名同学和他们的2名家长共17人也来购票,请你为他们设计出最省的购票方案,并求出此时的购票费用.
【答案】(1)学生人数为12-8=4人,成人人数为8人.
(2)购团体票更省钱.
(3)最省的购票方案为:买16人的团体票,再买13张学生票,此时的购票费用为644元.
【解析】
(1)设成人人数为x人,则学生人数为(12-x)人,可列出一元一次方程,即可解出学生人数和成人人数;
(2)先算出团购价所花的费用,与原价400比较即可选择方案;
(3)再加入17人进行购票,可先购买16人团体票,再购买学生票费用最少.
解:(1)设成人人数为x人,则学生人数为(12-x)人,则:
由题中所给的票价单可得:40x+ 20×(12-x)=400
解得:x=8
答:学生人数为12-8=4人,成人人数为8人.
(2)如果买团体票,按16人计算,共需费用:
40×0.6×16=384元
384<400
所以,购团体票更省钱.
(3)非团体票需要:10×40+20×19=780元
买16人的团体票,再买13张学生票,此时的购票费用为:16×40×0.6+13×20=644元.
∵644<780
∴最省的购票方案为:买16人的团体票,再买13张学生票.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+5x﹣2m=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若两个实数根分别为x1和x2,且x12+x22=23,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读下面材料:
点A,B在数轴上分别表示实数a,b,A,B两点之间的距离表示为|AB|.
当A,B两点中有一点在原点时,不妨设点A在原点,如图(1),|AB|=|OB|=|b|=|a﹣b|;当A,B两点都不在原点时,
①如图(2),点A,B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|;
②如图(3),点A,B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|;
③如图(4),点A,B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=|a﹣b|;
综上,数轴上A,B两点之间的距离|AB|=|a﹣b|.
(2)回答下列问题:
①数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示1和﹣3的两点之间的距离是 ;
②数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2,那么x为 ;
③当代数式|x+1|+|x﹣2|取最小值时,相应的x的取值范围是 .
④解方程|x+1|+|x﹣2|=5.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东东在研究数学问题时遇到一个定义:将三个已经排好顺序数:x1,x2,x3,称为数列x1,x2,x3.计算|x1|,![]() ,
,![]() ,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,
,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,![]() =
=![]() ,
,![]() =
=![]() ,所以数列2,-1,3的最佳值为
,所以数列2,-1,3的最佳值为![]() .
.
东东进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的最佳值.如数列-1,2,3的最佳值为![]() ;数列3,-1,2的最佳值为1;….经过研究,东东发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为
;数列3,-1,2的最佳值为1;….经过研究,东东发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)数列-4,-3,1的最佳值为
(2)将“-4,-3,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为 ,取得最佳值最小值的数列为 (写出一个即可);
(3)将2,-9,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的最佳值为1,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,第一象限内的点A、B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且tan∠ACB=![]()
求:(1)反比例函数的解析式;
(2)点C的坐标;
(3)sin∠ABC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OM是∠AOC的平分线.ON是∠BOC的平分线.
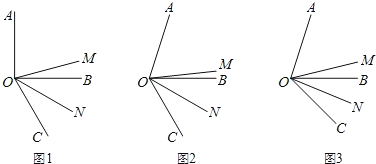
(1)如图1,当∠AOB=90°,∠BOC=60°时,∠MON的度数是多少?为什么?
(2)如图2,当∠AOB=70°,∠BOC=60°时,∠MON= (直接写出结果)
(3)如图3,当∠AOB=α,∠BOC=β时,猜想:∠MON﹣∠CON= (直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知A(![]() ,y1),B(2,y2)为反比例函数y=
,y1),B(2,y2)为反比例函数y=![]() 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )

A.(![]() ,0) B.(1,0) C.(
,0) B.(1,0) C.(![]() ,0) D.(
,0) D.(![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为奖励学习之星,准备在某商店购买A、B两种文具作为奖品,已知一件A种文具的价格比一件B种文具的价格便宜5元,且用600元买A种文具的件数是用400元买B种文具的件数的2倍.
(1)求一件A种文具的价格;
(2)根据需要,该校准备在该商店购买A、B两种文具共150件.
①求购买A、B两种文具所需经费W与购买A种文具的件数a之间的函数关系式;
②若购买A种文具的件数不多于B种文具件数的2倍,且计划经费不超过2750元,求有几种购买方案,并找出经费最少的方案,及最少需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
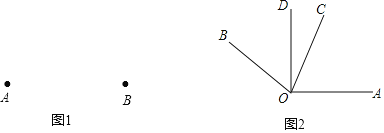
【题目】(1)已知:点A和点B(如图1),根据条件画图(用三角板和量角器):
①画射线BA;
②画∠ABC=90°,使得点C在线段AB上方且AB=BC;
③连接AC,画出∠ABC的角平分线BD,交AC于D.通过观察、度量、猜想获得线段BD、AC的关系.
(2)已知:如图2,∠AOB=150,OC平分∠AOB,AO⊥DO,求∠COD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com