
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是斜边
是斜边![]() 上的中线,以
上的中线,以![]() 为直径的
为直径的![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
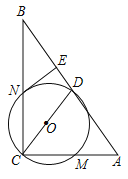
(1)若![]() 的半径为
的半径为![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)求证:![]() 与
与![]() 相切.
相切.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)由直角三角形的性质可求AB=26,由勾股定理可求BC=24,由等腰三角形的性质可得BN=12;
(2)欲证明NE为⊙O的切线,只要证明ON⊥NE即可.
(1)连接DN,ON

∵⊙O的半径为![]() ,
,
∴CD=13
∵∠ACB=90°,CD是斜边AB上的中线,
∴BD=CD=AD=13,
∴AB=26,
∴BC=![]()
∵CD为直径
∴∠CND=90°,且BD=CD
∴BN=NC=12
(2)∵∠ACB=90°,D为斜边的中点,
∴CD=DA=DB=![]() AB,
AB,
∴∠BCD=∠B,
∵OC=ON,
∴∠BCD=∠ONC,
∴∠ONC=∠B,
∴ON∥AB,
∵NE⊥AB,
∴ON⊥NE,
∴NE为⊙O的切线.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
【题目】如图l,在![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的动点,且
上的动点,且![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() ,
,![]() ,设
,设![]() ,
,![]() 的面积为
的面积为![]() ,图2是
,图2是![]() 关于
关于![]() 的函数图象,则下列说法不正确的是( )
的函数图象,则下列说法不正确的是( )
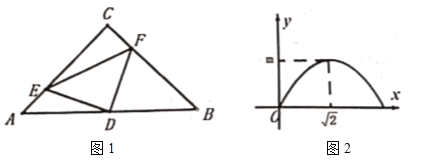
A.![]() 是等腰直角三角形B.
是等腰直角三角形B.![]()
C.![]() 的周长可以等于6D.四边形
的周长可以等于6D.四边形![]() 的面积为2
的面积为2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△BDE和△FGH是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC内.若求五边形DECHF的周长,则只需知道( )
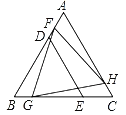
A.△ABC的周长B.△AFH的周长
C.四边形FBGH的周长D.四边形ADEC的周长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 为
为![]() 上一点,
上一点,![]() 和过点
和过点![]() 的切线互相垂直,垂足为
的切线互相垂直,垂足为![]() ,
,![]() 交
交![]() 于点
于点![]() ,直线
,直线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/22/2490290299265024/2493010512216064/STEM/6108b9d591da4e268d6d47ef4c154d16.png]
(1)求证:![]() 平分
平分![]() ;
;
(2)探究线段![]() ,
,![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(3)若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD内接于⊙O,AB=AC,BD为⊙O的直径,AE⊥BD,垂足为点E,交BC于点F.
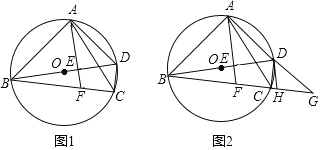
(1)求证:FA=FB;
(2)如图2,分别延长AD,BC交于点G,点H为FG的中点,连接DH,若tan∠ACB=![]() ,求证:DH为⊙O的切线;
,求证:DH为⊙O的切线;
(3)在(2)的条件下,若DA=3![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
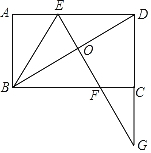
【题目】如图,已知矩形ABCD,对角线BD的垂直平分线分别交AD,BC和BD于点E,F,O.EF,DC的延长线交于点G,且OD=CG,连接BE.
(1)求证:△DOE≌△GCF;
(2)求证:BE平分∠ABD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着社会的发展,物质生活极大丰富,青少年的营养过剩,身体越来越胖,某校为了了解八年级学生的体重情况,随机抽取了八年级部分学生进行调查,将抽取学生的体重情况绘制成如下不完整的统计图表,如图表所示,请根据图表信息回答下列问题:
组别 | 体重(千克} | 人数 |
A |
| 3 |
B |
| 12 |
C |
| a |
D |
| 10 |
E |
| 8 |
F |
| 2 |
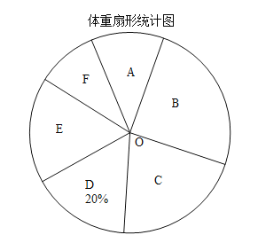
(1)求得![]() __________(直接写出结果); 在扇形统计图中,D组所在扇形的圆心角的度数等于_________ ;
__________(直接写出结果); 在扇形统计图中,D组所在扇形的圆心角的度数等于_________ ;
(2)调查的这组数据的中位数落在_________组;
(3)如果体重不低于55千克,属于偏胖,该校八年级有1200名学生,请估算该年级体重偏胖的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C(0,3),且抛物线的顶点坐标为(1,4).
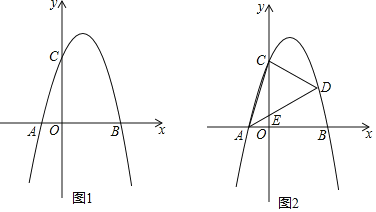
(1)求抛物线的解析式;
(2)如图2,点D是第一象限抛物线上的一点,AD交y轴于点E,设点D的横坐标为m,设△CDE的面积为S,求S与m的函数关系式(不必写出自变量的取值范围);
(3)在(2)的条件下,连接AC,是否存在这样的点D,使得∠DAB=2∠ACO,若存在,求点D的坐标及相应的S的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com