
【题目】如图l,在![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的动点,且
上的动点,且![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() ,
,![]() ,设
,设![]() ,
,![]() 的面积为
的面积为![]() ,图2是
,图2是![]() 关于
关于![]() 的函数图象,则下列说法不正确的是( )
的函数图象,则下列说法不正确的是( )
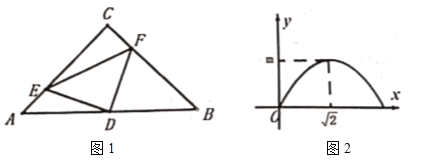
A.![]() 是等腰直角三角形B.
是等腰直角三角形B.![]()
C.![]() 的周长可以等于6D.四边形
的周长可以等于6D.四边形![]() 的面积为2
的面积为2
科目:初中数学 来源: 题型:
【题目】抛物线![]() (
(![]() ,
,![]() ,
,![]() 是常数,
是常数,![]() )经过点A(
)经过点A(![]() ,
,![]() )和点B (
)和点B (![]() ,
,![]() ),且抛物线的对称轴在
),且抛物线的对称轴在![]() 轴的左侧. 下列结论: ①
轴的左侧. 下列结论: ① ![]() ; ② 方程
; ② 方程![]() 有两个不等的实数根; ③
有两个不等的实数根; ③![]() . 其中,正确结论的个数是( ).
. 其中,正确结论的个数是( ).
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
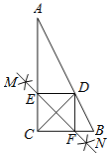
【题目】如图,Rt△ABC中,∠ACB=90°,CD平分∠ACB交AB于点D,按下列步骤作图:
步骤1:分别以点C和点D为圆心,大于![]() 的长为半径作弧,两弧相交于M,N两点;
的长为半径作弧,两弧相交于M,N两点;
步骤2:作直线MN,分别交AC,BC于点E,F;
步骤3:连接DE,DF.
若AC=4,BC=2,则线段DE的长为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
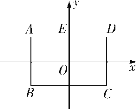
【题目】如图,在平面直角坐标系中,矩形![]() 的对称中心为坐标原点
的对称中心为坐标原点![]() ,
,![]() 轴于点
轴于点![]() (点
(点![]() 在点
在点![]() 的左侧),经过
的左侧),经过![]() 、
、![]() 两点的函数
两点的函数![]() 的图象记为
的图象记为![]() ,函数
,函数![]() 的图象记为
的图象记为![]() ,其中
,其中![]() 是常数,图象
是常数,图象![]() 、
、![]() 合起来得到的图象记为
合起来得到的图象记为![]() .设矩形
.设矩形![]() 的周长为
的周长为![]() .
.
(1)当点![]() 的横坐标为-1时,求
的横坐标为-1时,求![]() 的值;
的值;
(2)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)当![]() 与矩形
与矩形![]() 恰好有两个公共点时,求
恰好有两个公共点时,求![]() 的值;
的值;
(4)设![]() 在
在![]() 上最高点的纵坐标为
上最高点的纵坐标为![]() ,当
,当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
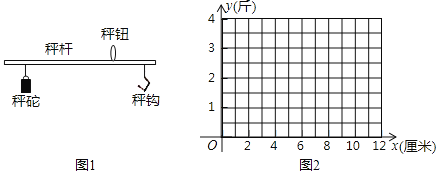
【题目】我国传统的计重工具﹣﹣秤的应用,方便了人们的生活.如图1,可以用秤砣到秤纽的水平距离,来得出秤钩上所挂物体的重量.称重时,若秤杆上秤砣到秤纽的水平距离为x(厘米)时,秤钩所挂物重为y(斤),则y是x的一次函数.下表中为若干次称重时所记录的一些数据.
x(厘米) | 1 | 2 | 4 | 7 | 11 | 12 |
y(斤) | 0.75 | 1.00 | 1.50 | 2.75 | 3.25 | 3.50 |
(1)在上表x,y的数据中,发现有一对数据记录错误.在图2中,通过描点的方法,观察判断哪一对是错误的?
(2)根据(1)的发现,问秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位需购买甲、乙两种消毒剂.经了解,这两种消毒剂的价格都有零售价和批发价(若按批发价,则每种消毒剂购买的数量不少于50桶),零售时甲种消毒剂每桶比乙种消毒剂多8元,已知购买两种消毒剂各![]() (
(![]() )桶,所需费用分别是960元、720元.
)桶,所需费用分别是960元、720元.
(1)求甲、乙两种消毒剂的零售价;
(2)该单位预计批发这两种消毒剂500桶,且甲种消毒剂的数量不少于乙种消毒剂数量的![]() ,甲、乙两种消毒剂的批发价分别为20元/桶、16元/桶.设甲种消毒剂批发数量为
,甲、乙两种消毒剂的批发价分别为20元/桶、16元/桶.设甲种消毒剂批发数量为![]() 桶,购买资金总额为
桶,购买资金总额为![]() (元),请写出
(元),请写出![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最小值和此时的购买方案.
的最小值和此时的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了一次创建全国文明城市知识竞赛活动,有30名同学参加这次竞赛,成绩分布频数表如下:(单位:分)
成绩(分) | 组中值 | 频数(人数) |
80.5~85.5 | 83 | 3 |
85.5~90.5 | 88 | 6 |
90.5~95.5 | 93 | 12 |
95.5~100.5 | 98 | 9 |
(1)利用组中值计算这30位同学的平均数;
(2)学校根据这次竞赛成绩从高到低选15位同学参加市级比赛,小明同学也参加了这次竞赛,知道自己的成绩后,他想知道自己是否有资格参加市里比赛(学校还未公布到市里比赛名单),他最应关注频数,平均分,众数,中位数中的哪个量?请说明理由;
(3)“创文知识竞赛”中,获一等奖的小红同学得到了印有龚扇、剪纸、彩灯图案的三枚纪念章,她从中选取两枚送给弟弟,则小红送给弟弟的两枚纪念章中,恰好有彩灯图案的概率是多少?请用树状图或列表法说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某无人机于空中![]() 处探测到目标
处探测到目标![]() 的俯角分别是
的俯角分别是![]() ,此时无人机的飞行高度
,此时无人机的飞行高度![]() 为
为![]() ,随后无人机从
,随后无人机从![]() 处继续水平飞行
处继续水平飞行![]() m到达
m到达![]() 处.
处.
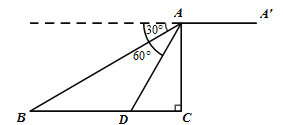
(1)求![]() 之间的距离
之间的距离
(2)求从无人机![]() 上看目标
上看目标![]() 的俯角的正切值.
的俯角的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com