练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在平行四边形ABCD中，点E，F分别在AB、CD上，AE=CF ，且DF=BF； 求证:四边形DEBF为菱形。

    【答案】证明见解析

    【解析】分析：已知四边形ABCD是平行四边形，根据平行四边形的性质可得CD∥AB，且CD=AB，又因CF=AE，可得DF=BE，根据一组对标平行且相等的四边形为平行四边形可得四边形DEBF是平行四边形，由DF=BF，根据一组邻边相等的平行四边形为菱形，即可判定平行四边形DEBF是菱形.

    详解：

    ∵四边形ABCD是平行四边形，

    ∴CD∥AB，且CD=AB，

    又CF=AE，

    ∴CD-CF=AB-AE，

    即DF=BE，

    又DF∥BE，

    ∴四边形DEBF是平行四边形，

    又DF=BF，

    ∴平行四边形DEBF是菱形.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】筐葡萄，以每筐千克为标准，超过或不足的千克数分别用正、负数来表示，与标准质量的差值记录如下：

    单位（千克）

    筐数

    （1）筐葡萄中，最重的一筐比最轻的一筐重________千克．

    （2）与标准重量比较，筐葡萄总计超过或不足多少千克？

    （3）若葡萄每千克售价元，则出售这筐葡萄可卖多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线与x轴、y轴分别交于点A，B，点C是线段AB上一点，四边形OADC是菱形，求OD的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：O是直线AB上的一点，是直角，OE平分．

    （1）如图1．若．求的度数；

    （2）在图1中，，直接写出的度数（用含a的代数式表示）；

    （3）将图1中的绕顶点O顺时针旋转至图2的位置，探究和的度数之间的关系．写出你的结论，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AB=5，AD=3，点P是AB边上一点（不与A，B重合），连接CP，过点P作PQ⊥CP交AD于点Q，连接CQ。取CQ的中点M，连接MD，MP，若MD⊥MP，则AQ的长________。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

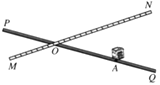
    【题目】如图，铁路MN和公路PQ在点O处交汇，∠QON=30°.公路PQ上A处距O点240米．如果火车行驶时，周围200米以内会受到噪音的影响．那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时，A处受噪音影响的时间为（）

    A. 秒 B. 16秒 C. 秒 D. 24秒

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，正方形OABC的顶点O在原点。

    （1）如图①，点C的坐标为（，），且实数，满足，求C点的坐标及线段0C的长度；

    （2）如图②，点F在BC上，AB交x轴于点E，EF，OC的延长线交于点G，EG=OG，求∠EOF的度数；

    （3）如图③，将（1）中正方形OABC绕点O顺时针旋转，使OA落在y轴上，E为AB上任意一点，OE的垂直平分线交x轴于点G，交OE于点P,连接EG交BC于点F，求△BEF的周长。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 如图，已知△ABC，AB=AC=1，∠A=36°，∠ABC的平分线BD交AC于点D，则AD的长是 ， cosA的值是 ． （结果保留根号）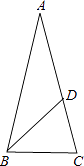

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】商店只有雪碧、可乐、果汁、奶汁四种饮料，每种饮料数量充足，某同学去该店购买饮料，每种饮料被选中的可能性相同．
    （1）若他去买一瓶饮料，则他买到奶汁的概率是；
    （2）若他两次去买饮料，每次买一瓶，且两次所买饮料品种不同，请用树状图或列表法求出他恰好买到雪碧和奶油的概率．

    查看答案和解析>>

    同步练习册答案