
【题目】如图,在矩形ABCD中,AB=5,AD=3,点P是AB边上一点(不与A,B重合),连接CP,过点P作PQ⊥CP交AD于点Q,连接CQ。取CQ的中点M,连接MD,MP,若MD⊥MP,则AQ的长________。

【答案】2
【解析】分析:如图,过M作EF⊥CD于F,则EF⊥AB,证得△MDF≌△PME,求得ME=![]() ,再利用梯形的中位线定理求解即可.
,再利用梯形的中位线定理求解即可.
详解:
如图,过M作EF⊥CD于F,则EF⊥AB,

∵MD⊥MP,
∴∠PMD=90°,
∴∠PME+∠DMF=90°,
∵∠FDM+∠DMF=90°,
∴∠MDF=∠PME,
∵M是QC的中点,
根据直角三角形斜边上的中线性质求得DM=PM=![]() QC,
QC,
在△MDF和△PME中, ,
,
∴△MDF≌△PME(AAS),
∴ME=DF,PE=MF,
∵EF⊥CD,AD⊥CD,
∴EF∥AD,
∵QM=MC,
∴DF=CF=![]() DC=
DC=![]() ;
;
∴ME=![]() ,
,
∵ME是梯形ABCQ的中位线,
∴2ME=AQ+BC,即5=AQ+3,
∴AQ=2.
故答案为:2.


科目:初中数学 来源: 题型:
【题目】某自行车厂一周计划每日生产![]() 辆自行车,由于人数和操作原因,每日实际生产量分别为
辆自行车,由于人数和操作原因,每日实际生产量分别为![]() 辆、
辆、![]() 辆、
辆、![]() 辆、
辆、![]() 辆、
辆、![]() 辆、
辆、![]() 辆、
辆、![]() 辆.
辆.
![]() 用正负数表示每日实际生产量与计划量的增减情况;
用正负数表示每日实际生产量与计划量的增减情况;
![]() 该车厂本周实际共生产多少辆自行车?平均每日实际生产多少辆自行车?
该车厂本周实际共生产多少辆自行车?平均每日实际生产多少辆自行车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为4,将此正方形置于平面直角坐标系中,使AB边落在X轴的正半轴上,且A点的坐标是(1,0).
(1)直线![]() 经过点C,且与x轴交与点E,求四边形AECD的面积;
经过点C,且与x轴交与点E,求四边形AECD的面积;
(2)若直线l经过点E,且将正方形ABCD分成面积相等的两部分,求直线l的解析式;
(3)若直线l1经过点F(﹣![]() ,0),且与直线y=3x平行,将(2)中直线l沿着y轴向上平移
,0),且与直线y=3x平行,将(2)中直线l沿着y轴向上平移![]() 个单位交轴x于点M,交直线l1于点N,求△NMF的面积.
个单位交轴x于点M,交直线l1于点N,求△NMF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
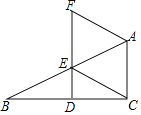
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AP垂直∠ABC的平分线BP于点P.若△ABC的面积为32cm2,BP=6cm,且△APB的面积是△APC的面积的3倍.则AP=________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,经过原点的抛物线的解析式可以是y=ax2+bx(a≠0)
(1)对于这样的抛物线:
当顶点坐标为(1,1)时,a=;
当顶点坐标为(m,m),m≠0时,a与m之间的关系式是
(2)继续探究,如果b≠0,且过原点的抛物线顶点在直线y=kx(k≠0)上,请用含k的代数式表示b;
(3)现有一组过原点的抛物线,顶点A1 , A2 , …,An在直线y=x上,横坐标依次为1,2,…,n(为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1 , B2 , …,Bn , 以线段AnBn为边向右作正方形AnBnCnDn , 若这组抛物线中有一条经过Dn , 求所有满足条件的正方形边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com