
【题目】若x1、x2是关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:![]() ,
,![]() .我们把它们称为根与系数关系定理.
.我们把它们称为根与系数关系定理.
如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:AB=![]() =
=![]() =
=![]() =
=![]() =
=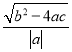
请你参考以上定理和结论,解答下列问题:
设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.
(1)当△ABC为等腰直角三角形时,直接写出b2-4ac的值;
(2)当△ABC为等腰三角形,且∠ACB=120°时,直接写出b2-4ac的值;
(3)设抛物线y=x2+mx+5与x轴的两个交点为A、B,顶点为C,且∠ACB=90°,试问如何平移此抛物线,才能使∠ACB=120°.
【答案】(1)4;(2)![]() ;(3)抛物线
;(3)抛物线![]() 向上平移
向上平移![]() 个单位后,向左或向右平移任意个单位都能使得
个单位后,向左或向右平移任意个单位都能使得![]() 度数由90°变为120°.
度数由90°变为120°.
【解析】
(1)根据上述结论及直角三角形的性质列出等式,计算出即可;
(2)根据上述结论及含120°的等腰三角形的边角关系,列出方程,解出方程即可;
(3)根据(1)中结论,计算出m的值,设出平移后的函数解析式,根据(2)中结论,列出等量关系即可解出.
解:(1)由 y=ax2+bx+c(a≠0)可知顶点C![]()
∵![]() ,
,
∴当△ABC为等腰直角三角形时,根据直角三角形斜边上的中线等于斜边的一半可知:![]() =
=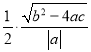 ,化简得
,化简得![]()
故答案为:4
(2) 由 y=ax2+bx+c(a≠0)可知顶点C![]()
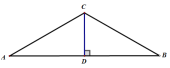
如图,过点C作CD⊥AB交AB于点D,
∵∠ACB=120°,∴∠A=30°
∵tan30°=![]() ,
,
即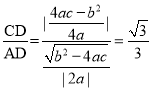 ,又因为
,又因为![]() ,
,
∴化简得![]()
故答案为:![]()
(3)∵![]()
![]()
![]()
因为向左或向右平移时![]() 的度数不变,
的度数不变,
所以只需将抛物线![]() 向上或向下平移使
向上或向下平移使![]() ,然后向左或向右平移任意个单位即可.
,然后向左或向右平移任意个单位即可.
设向上或向下平移后的抛物线的解析式为:![]() ,
,
平移后![]() ,
,
![]()
所以,抛物线![]() 向上平移
向上平移![]() 个单位后,向左或向右平移任意个单位都能使得
个单位后,向左或向右平移任意个单位都能使得![]() 度数由
度数由![]() 变为
变为![]() .
.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:初中数学 来源: 题型:
【题目】如图所示是我国古代城市用以滞洪或分洪系统的局部截面原理图,图中![]() 为下水管道口直径,
为下水管道口直径,![]() 为可绕转轴
为可绕转轴![]() 自由转动的阀门,平时阀门被管道中排出的水冲开,可排出城市污水:当河水上涨时,阀门会因河水压迫而关闭,以防止河水倒灌入城中.若阀门的直径
自由转动的阀门,平时阀门被管道中排出的水冲开,可排出城市污水:当河水上涨时,阀门会因河水压迫而关闭,以防止河水倒灌入城中.若阀门的直径![]() ,
,![]() 为检修时阀门开启的位置,且
为检修时阀门开启的位置,且![]() .
.
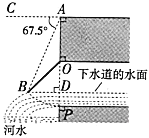
(1)直接写出阀门被下水道的水冲开与被河水关闭过程中![]() 的取值范围;
的取值范围;
(2)为了观测水位,当下水道的水冲开阀门到达![]() 位置时,在点
位置时,在点![]() 处测得俯角
处测得俯角![]() ,若此时点
,若此时点![]() 恰好与下水道的水平面齐平,求此时下水道内水的深度.(结果保留根号)
恰好与下水道的水平面齐平,求此时下水道内水的深度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
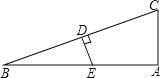
【题目】已知如图所示,在Rt△ABC中,∠A=90°,∠BCA=75°,AC=8cm,DE垂直平分BC,则BE的长是( )
A.4cmB.8cmC.16cmD.32cm
查看答案和解析>>
科目:初中数学 来源: 题型:
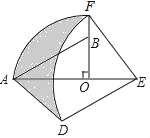
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
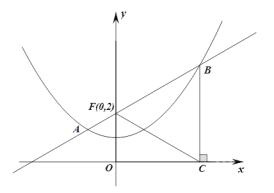
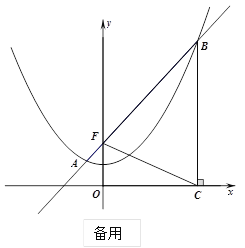
【题目】如图,已知抛物线![]() 过点
过点![]() ,过定点
,过定点![]() 的直线
的直线![]() :
:![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点,点
两点,点![]() 在点
在点![]() 的右侧,过点
的右侧,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() .
.
(1)求抛物线的解析式;
(2)设点![]() 在x轴上运动,连接
在x轴上运动,连接![]() ,作
,作![]() 的垂直平分线与过点D作x轴的垂线交于点
的垂直平分线与过点D作x轴的垂线交于点![]() ,判断点
,判断点![]() 是否在抛物线
是否在抛物线![]() 上,并证明你的判断;
上,并证明你的判断;
(3)若![]() ,设
,设![]() 的中点为
的中点为![]() ,抛物线上是否存在点
,抛物线上是否存在点![]() ,使得
,使得![]() 周长最小,若存在求出周长的最小值,若不存在说明理由;
周长最小,若存在求出周长的最小值,若不存在说明理由;
(4)若![]() ,在抛物线上是否存在点
,在抛物线上是否存在点![]() ,使得
,使得![]() 的面积为
的面积为![]() ,若存在求出点
,若存在求出点![]() 的坐标,若不存在说明理由.
的坐标,若不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
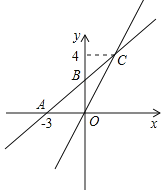
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交于点A(﹣3,0),与y轴交于点B,且与正比例函数y=![]() x的图象交点为C(m,4).
x的图象交点为C(m,4).
(1)求一次函数y=kx+b的解析式;
(2)求△BOC的面积;
(3)若点D在第二象限,△DAB为等腰直角三角形,则点D的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E为AB上一动点(不与A、B重合).将△EBC沿CE翻折至△EFC,延长EF交边AD于点G.
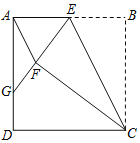
(1)连结AF,若AF∥CE.证明:点E为AB的中点;
(2)证明:GF=GD;
(3)若AD=5,设EB=x,GD=y,求y与x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0,a、b、c为常数)上部分点的横坐标x,纵坐标y的对应值如下表:
x | …… | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | …… |
y | …… |
| 4 |
| 4 | m | 0 | …… |
则下列结论中:①抛物线的对称轴为直线x=﹣1;②m=![]() ;③当﹣4<x<2时,y<0;④方程ax2+bx+c﹣4=0的两根分别是x1=﹣2,x2=0,其中正确的个数有( )
;③当﹣4<x<2时,y<0;④方程ax2+bx+c﹣4=0的两根分别是x1=﹣2,x2=0,其中正确的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
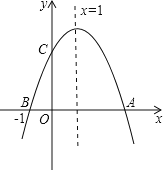
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0),则下面的四个结论,其中正确的个数为( )
①2a+b=0②4a﹣2b+c<0③ac>0④当y>0时,﹣1<x<4
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com