
【题目】抛物线y=ax2+bx+c(a≠0,a、b、c为常数)上部分点的横坐标x,纵坐标y的对应值如下表:
x | …… | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | …… |
y | …… |
| 4 |
| 4 | m | 0 | …… |
则下列结论中:①抛物线的对称轴为直线x=﹣1;②m=![]() ;③当﹣4<x<2时,y<0;④方程ax2+bx+c﹣4=0的两根分别是x1=﹣2,x2=0,其中正确的个数有( )
;③当﹣4<x<2时,y<0;④方程ax2+bx+c﹣4=0的两根分别是x1=﹣2,x2=0,其中正确的个数有( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
①根据表格中x与y的对应值和函数的对称性,可得出函数的对称轴;
②函数的对称轴为:x=-1,则m和![]() 对应,即可求解;
对应,即可求解;
③当x=2时y=0,根据函数的对称性,x=-4,y=0,而当-4<x<2时,y>0,即可求解;
④方程ax2+bx+c-4=0的两根,就是y=ax2+bx+c和y=4的两图像的交点的横坐标,即可求解.
解:①根据表格可得,函数的对称轴为:x=-1,此时y=![]() ,故①符合题意;
,故①符合题意;
②函数的对称轴为:x=-1,则m和![]() 对应,故②符合题意;
对应,故②符合题意;
③∵x=2,y=0,∴根据函数的对称性,x=-4,y=0,∴当-4<x<2时,y>0,故③不符合题意;
④∵ax2+bx+c-4=0,∴ax2+bx+c=4∴方程ax2+bx+c-4=0的两根,就是y=ax2+bx+c和y=4的两图像的交点的横坐标∴x1=﹣2,x2=0,故④符合题意,
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,△ADF按顺时针方向旋转一定角度后得到△ABE,点E落在AD边上,若AF=4.AB=7.
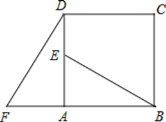
(1)旋转中心为 ;旋转角度为 ;
(2)求DE的长度;
(3)指出BE与DF的关系如何?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0; ②b2-4ac<0 ; ③2a+b>0 ;④a+b+c>0,其中正确的个数( )
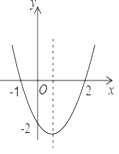
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自行车因其便捷环保深受人们喜爱,成为日常短途代步与健身运动首选.如图1是某品牌自行车的实物图,图2是它的简化示意图.经测量,车轮的直径为66cm,车座B到地面的距离BE为90cm,中轴轴心C到地面的距离CF为33cm,车架中立管BC的长为60cm,后轮切地面L于点D.(参考数据:sin72≈0.95,cos18°≈0.95,tan43.5°≈0.9 5)
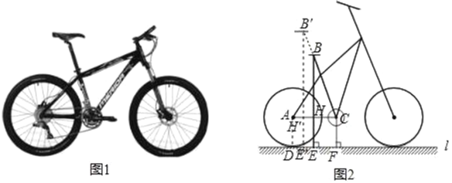
(1)求∠ACB的大小(精确到1°)
(2)如果希望车座B到地面的距离B'E′为96.8cm,车架中立管BC拉长的长度BB′应是多少?(结果取整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在小水池旁有一盏路灯,已知支架AB的长是0.8m,A端到地面的距离AC是4m,支架AB与灯柱AC的夹角为65°.小明在水池的外沿D测得支架B端的仰角是45°,在水池的内沿E测得支架A端的仰角是50°(点C、E、D在同一直线上),求小水池的宽DE.(结果精确到0.1m)(sin65°≈0.9,cos65°≈0.4,tan50°≈1.2)

查看答案和解析>>
科目:初中数学 来源: 题型:
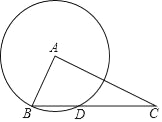
【题目】如图,已知Rt△ABC,∠BAC=90°,BC=5,AC=2![]() ,以A为圆心、AB为半径画圆,与边BC交于另一点D.
,以A为圆心、AB为半径画圆,与边BC交于另一点D.
(1)求BD的长;
(2)连接AD,求∠DAC的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣4和y=﹣ax2+4都经过x轴上的A、B两点,两条抛物线的顶点分别为C、D.当四边形ACBD的面积为40时,a的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE是⊙O的直径,点A在EB的延长线上,弦PD⊥BE,垂足为C,连接OD,
∠AOD=∠APC.
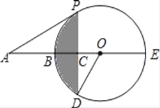
(1)求证:AP是⊙O的切线;
(2)若⊙O的半径是4,AP=4![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠C=90°,AC=6,BC=8,点P以每秒1个单位的速度从A向C运动,同时点Q以每秒2个单位的速度从B向A方向运动,Q到达A点后,P点也停止运动,设点P,Q运动的时间为t秒.
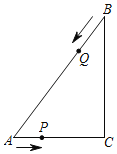
(1)求P点停止运动时,BP的长;
(2)P,Q两点在运动过程中,点E是Q点关于直线AC的对称点,是否存在时间t,使四边形PQCE为菱形?若存在,求出此时t的值;若不存在,请说明理由.
(3)P,Q两点在运动过程中,求使△APQ与△ABC相似的时间t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com