
����Ŀ����ͼ����֪Rt��ABC�У���C��90����AC��6��BC��8����P��ÿ��1����λ���ٶȴ�A��C�˶���ͬʱ��Q��ÿ��2����λ���ٶȴ�B��A�����˶���Q����A���P��Ҳֹͣ�˶������P��Q�˶���ʱ��Ϊt�룮
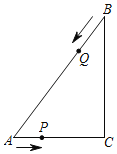
��1����P��ֹͣ�˶�ʱ��BP�ij���
��2��P��Q�������˶������У���E��Q�����ֱ��AC�ĶԳƵ㣬�Ƿ����ʱ��t��ʹ�ı���PQCEΪ���Σ������ڣ������ʱt��ֵ���������ڣ���˵�����ɣ�
��3��P��Q�������˶������У���ʹ��APQ����ABC���Ƶ�ʱ��t��ֵ��
���𰸡���1��![]() ����2�����ڣ�t��
����2�����ڣ�t��![]() sʱ���ı���PQCE�����Σ���3��t��ֵΪ
sʱ���ı���PQCE�����Σ���3��t��ֵΪ![]() s��
s��![]() sʱ��APQ����ABC����
sʱ��APQ����ABC����
��������
��1�������Q�Ĵ�B��A���˶�ʱ�䣬�����AP�ij������ù��ɶ������ɽ�����⣮
��2����ͼ1�У����ı���PQCE������ʱ������QE��AC��K����QD��BC��D������DQ��CK���������̼��ɽ�����⣮
��3�����������Σ���ͼ3��1�У�����APQ��90��ʱ����ͼ3��2�У�����AQP��90��ʱ���ֱ����̼��ɽ�����⣮
�⣺��1����Rt��ABC�У��ߡ�C��90����AC��6��BC��8��
��AB��![]() ��10��
��10��
��Q�˶�����Aʱ��t��![]() ��5��
��5��
��AP��5��PC��1��
��Rt��PBC��PB��![]() ��
��![]() ��
��
��2����ͼ1�У����ı���PQCE������ʱ������QE��AC��K����QD��BC��D��
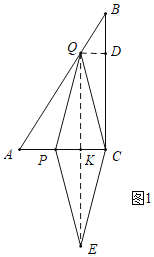
���ı���PQCE�����Σ�
��PC��EQ��PK��KC��
�ߡ�QKC����QDC����DCK��90����
���ı���QDCK�Ǿ��Σ�
��DQ��CK��
��![]() 2t��
2t��![]() ��6��t����
��6��t����
���t��![]() ��
��
��t��![]() sʱ���ı���PQCE�����Σ�
sʱ���ı���PQCE�����Σ�
��3����ͼ3��1�У�����APQ��90��ʱ��
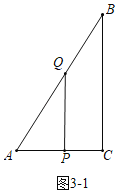
�ߡ�APQ����C��90����
��PQ��BC��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��t��![]() ��
��
��ͼ3��2�У�����AQP��90��ʱ��
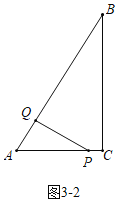
�ߡ�AQP�ס�ACB��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��t��![]() ��
��
����������t��ֵΪ![]() s��
s��![]() sʱ��APQ����ABC���ƣ�
sʱ��APQ����ABC���ƣ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y��ax2+bx+c��a��0��a��b��cΪ�������ϲ��ֵ�ĺ�����x��������y�Ķ�Ӧֵ���±���
x | ���� | ��3 | ��2 | ��1 | 0 | 1 | 2 | ���� |
y | ���� |
| 4 |
| 4 | m | 0 | ���� |
�����н����У��������ߵĶԳ���Ϊֱ��x����1����m��![]() ���۵���4��x��2ʱ��y��0���ܷ���ax2+bx+c��4��0�������ֱ���x1����2��x2��0��������ȷ�ĸ����У�������
���۵���4��x��2ʱ��y��0���ܷ���ax2+bx+c��4��0�������ֱ���x1����2��x2��0��������ȷ�ĸ����У�������
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
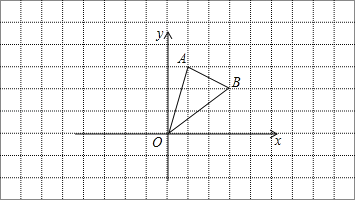
����Ŀ����ͼ���ڱ߳�Ϊ1��С�����������У���AOB�Ķ�����ڸ���ϣ�
(1)����AOB����ƽ��4����λ���ȵõ���A1O1B1���뻭����A1O1B1��
(2)�Ե�AΪ�Գ����ģ��뻭���� AOB���ڵ�A�����ĶԳƵ��� A O2 B2����д��B2�����ꣻ
(3)��ԭ��OΪ��ת���ģ��뻭������AOB��˳ʱ����ת90����ͼ����A2 O B3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ�У�C��0��4����AΪx����һ���㣬����AC����AC��A��˳ʱ����ת90��õ�AB������A��x�����˶�ʱ��OB+BC����СֵΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��x�ύ�ڵ�C����y�ύ�ڵ�B��������
��x�ύ�ڵ�C����y�ύ�ڵ�B��������![]() ����B��C���㣮
����B��C���㣮
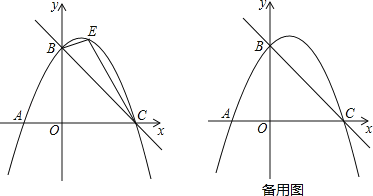
��1���������ߵĽ���ʽ��
��2����ͼ����E���������ϵ�һ���㣨����B��C�����غϣ�����BEC�����ΪS��Sȡ��ֵʱ����Ӧ�ĵ�E����ֻ��������
��3��ֱ��x=2��ֱ��BC�ڵ�M����Q�������߶Գ����ϵĶ��㣬�����������Ƿ���ڵ�P��ʹ����P��Q��A��MΪ������ı�����ƽ���ı��Σ�������ڣ���ֱ��д����P�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
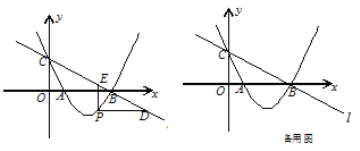
����Ŀ����ͼ��ֱ��![]() ��
�� ![]() ��
��![]() �ᡢ
�ᡢ![]() ��ֱ��ڵ�B��C������B��C�����������
��ֱ��ڵ�B��C������B��C�����������![]() ��
��![]() �����һ������ΪA��
�����һ������ΪA��
��1����������ߵĽ���ʽ��
��2������P��ֱ��![]() �·����������ϣ�����P��PD��
�·����������ϣ�����P��PD��![]() �ύ
�ύ![]() �ڵ�D��PE��
�ڵ�D��PE��![]() �ύ
�ύ![]() �ڵ�E��
�ڵ�E��
��PD+PE�����ֵ��
��3����FΪֱ��![]() �ϵĵ㣬��A��B��P��FΪ������ı����ܷ�ƽ���ı��Σ����ܣ������F�����ꣻ�����ܣ���˵�����ɣ�
�ϵĵ㣬��A��B��P��FΪ������ı����ܷ�ƽ���ı��Σ����ܣ������F�����ꣻ�����ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC��2����BAC��30�㣬����ABC��AC���۵õ���ACD���ӳ�AD��BC���ӳ����ڵ�E�����ABE�����Ϊ��������
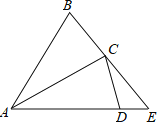
A.![]() B.
B.![]() C.3D.
C.3D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
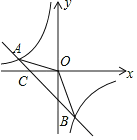
����Ŀ����֪A����4��2����B��n����4��������һ�κ���y=kx+b�ͷ���������y=![]() ͼ����������㣮
ͼ����������㣮
��1����һ�κ����ͷ����������Ľ���ʽ��
��2������AOB�������
��3���۲�ͼ��ֱ��д������ʽkx+b��![]() ��0�Ľ⼯��
��0�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һԪ���η�����ʵ������Ϊ��4���ǣ� ��
A. x2+2x��4=0 B. x2��4x+4=0 C. x2+4x+10=0 D. x2+4x��5=0
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com