
【题目】平面直角坐标系中,C(0,4),A为x轴上一动点,连接AC,将AC绕A点顺时针旋转90°得到AB,当点A在x轴上运动时,OB+BC的最小值为_____.

【答案】![]()
【解析】
过点B作BE⊥x轴,由旋转可知AC=AB,易证△ACO≌△BAE,则AE=OC=4,OA=BE,作点O关于BE的对称点D,则BE垂直平分OD,得到OB=BD,当点C、B、D三点共线时OB+BC=BD+BC=CD,然后设点A坐标为(x,0),则OA=x(![]() ),则点E为(x+4,0),则点D为(2x+8,0),得到OD=2x+8,利用勾股定理求出CD,结合二次函数的性质,即可得到CD的最小值,即可解决问题.
),则点E为(x+4,0),则点D为(2x+8,0),得到OD=2x+8,利用勾股定理求出CD,结合二次函数的性质,即可得到CD的最小值,即可解决问题.
解:过点B作BE⊥x轴,
∴∠AEB=∠COA=90°,
∵将AC绕A点顺时针旋转90°得到AB,
∴∠CAB=90°,AC=AB,
∴∠OCA+∠CAO=∠CAO+∠BAE=90°,
∴∠OCA=∠BAE,
∴△ACO≌△BAE,
∴CO=AE=4,OA=BE,
如图,作点O关于BE的对称点D,则BE垂直平分OD,
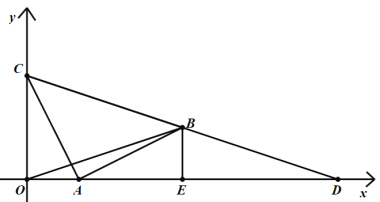
∴OB=DB,
∴当点C、B、D三点共线时OB+BC=BD+BC=CD,OB+BC的最小值为CD;
设点A坐标为(x,0),则OA=x(![]() ),
),
∴点E为(x+4,0),则点D为(2x+8,0),
∴OD=2x+8,
在直角三角形OCD中,由勾股定理,得:![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴当![]() 时,CD有最小值,
时,CD有最小值,
CD的最小值为:![]() ,
,
∴OB+BC的最小值为:![]() .
.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】自行车因其便捷环保深受人们喜爱,成为日常短途代步与健身运动首选.如图1是某品牌自行车的实物图,图2是它的简化示意图.经测量,车轮的直径为66cm,车座B到地面的距离BE为90cm,中轴轴心C到地面的距离CF为33cm,车架中立管BC的长为60cm,后轮切地面L于点D.(参考数据:sin72≈0.95,cos18°≈0.95,tan43.5°≈0.9 5)
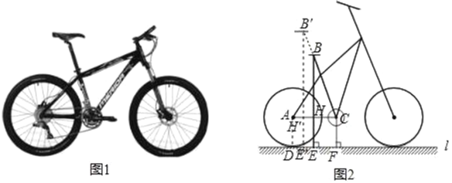
(1)求∠ACB的大小(精确到1°)
(2)如果希望车座B到地面的距离B'E′为96.8cm,车架中立管BC拉长的长度BB′应是多少?(结果取整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE是⊙O的直径,点A在EB的延长线上,弦PD⊥BE,垂足为C,连接OD,
∠AOD=∠APC.
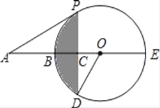
(1)求证:AP是⊙O的切线;
(2)若⊙O的半径是4,AP=4![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】圆O的半径为![]() ,点M的坐标为(m,3),若在圆O上存在一点N, 以M、N为正方形的两个顶点,且正方形的边均与两条坐标轴垂直,则m的最小值为_________
,点M的坐标为(m,3),若在圆O上存在一点N, 以M、N为正方形的两个顶点,且正方形的边均与两条坐标轴垂直,则m的最小值为_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某店代理某品牌商品的销售.已知该品牌商品进价每件40元,日销售y(件)与销售价x(元/件)之间的关系如图所示(实线),付员工的工资每人每天100元,每天还应支付其它费用150元.

(1)求日销售y(件)与销售价x(元/件)之间的函数关系式;
(2)该店员工人共3人,若某天收支恰好平衡(收入=支出),求当天的销售价是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2﹣2ax﹣3(a≠0)与x轴交于A,B两点(点A在点B左侧).

(1)求抛物线的对称轴;
(2)若AB=4,求该抛物线的解析式;
(3)若AB≤4,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠C=90°,AC=6,BC=8,点P以每秒1个单位的速度从A向C运动,同时点Q以每秒2个单位的速度从B向A方向运动,Q到达A点后,P点也停止运动,设点P,Q运动的时间为t秒.
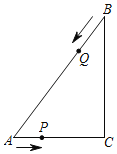
(1)求P点停止运动时,BP的长;
(2)P,Q两点在运动过程中,点E是Q点关于直线AC的对称点,是否存在时间t,使四边形PQCE为菱形?若存在,求出此时t的值;若不存在,请说明理由.
(3)P,Q两点在运动过程中,求使△APQ与△ABC相似的时间t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校初二体育考试选择项目中,选择篮球项目和排球项目的学生比较多.为了解学生掌握篮球技巧和排球技巧的水平况,进行了抽样调查,过程如下,请补充完整下题表格.
收集数据:从选择篮球和排球的学生各随机抽取10人,进行了测试,测试成绩如下:
排球9 9.5 9 9 8 10 9.5 8 4 9.5
篮球9.5 9.5 8.5 8.5 10 9.5 6 8 6 9
整理、描述数据:按如下分数段整理、描述这两组样本数据:
项目 人数 成绩x | 4.0≤x<5.5 | 5.5≤x<7.0 | 7.0≤x<8.5 | 8.5≤x<10 | 10 |
排球 | 1 | 0 | 2 | 6 | 1 |
篮球 | 0 | 2 | 1 | 6 | 1 |
(说明:成绩8.5分及以上为优秀,6分及以上为合格,6分以下为不合格.)
分折数据两组样本数据的平均数、中位数、众数如表所示:
项目 | 平均数 | 中位数 | 众数 |
排球 | 8.55 | a | 9和9.5 |
篮球 | 8.45 | 8.75 | b |
应用数据
(1)填空:a= ,b= .
p>(2)初三年级的小伟和小明看到上面数据后,小伟说:排球项目整体水平较高:小明说:篮球项目整体水平较高.你同意 的看法,理由为:① ;② .(从两个不同的角度说明推理的合理性)(3)如果初二年级有180人选排球项目,请信计该年级排球项目获得优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年九月是开学季,大多数学生会购买若干笔记本满足日常学习需要,校外某文具店老板开学前某日去批发市场进货,购进甲乙丙三种不同款式的笔记本共950本,已知甲款笔记本的进价为2元/本,乙款笔记本的进价是4元/本,丙款笔记本的进价是6元/本.
(1)本次进货共花费3300元,并且甲款的笔记本数量是乙款笔记本数量的2倍,请问本次购进丙款笔记本多少本?
(2)经过调研发现,甲款笔记本、乙款笔记本和丙款笔记本的零售价分别定为4元/本、6元/本和10元/本时,每天可分别售出甲款笔记本30本,乙款笔记本50本和丙款笔记本20本.如果将乙款笔记本的零售价提高![]() 元(a>25),甲款笔记本和丙款笔记本的零售价均保持不变,那么乙款笔记本每天的销售量将下降a%,丙款笔记本每天的销售量将上升
元(a>25),甲款笔记本和丙款笔记本的零售价均保持不变,那么乙款笔记本每天的销售量将下降a%,丙款笔记本每天的销售量将上升![]() a%,甲款笔记本每天的销量仍保持不变;若调价后每天销售三款笔记本共可获利260元,求a的值.
a%,甲款笔记本每天的销量仍保持不变;若调价后每天销售三款笔记本共可获利260元,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com