
【题目】自行车因其便捷环保深受人们喜爱,成为日常短途代步与健身运动首选.如图1是某品牌自行车的实物图,图2是它的简化示意图.经测量,车轮的直径为66cm,车座B到地面的距离BE为90cm,中轴轴心C到地面的距离CF为33cm,车架中立管BC的长为60cm,后轮切地面L于点D.(参考数据:sin72≈0.95,cos18°≈0.95,tan43.5°≈0.9 5)
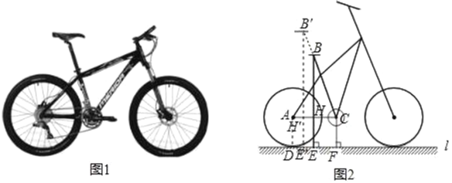
(1)求∠ACB的大小(精确到1°)
(2)如果希望车座B到地面的距离B'E′为96.8cm,车架中立管BC拉长的长度BB′应是多少?(结果取整数)
【答案】(1)∠ACB=72°;(2)车架中立管BC拉长的长度BB'应是7cm.
【解析】
(1)根据矩形的判定可得:四边形ADFC是矩形,从而求出BH,利用sin∠BCH=![]() ,即可求出∠BCH;
,即可求出∠BCH;
(2)设B'E'与AC交于点H',根据平行可证:B'H'∥BH,从而列出比例式即可求出B'C,从而求出BB′的长度.
(1)∵AD⊥l,CF⊥l,HE⊥l
∴AD∥CF∥HE,
∵AD=33cm,CF=33cm,
∴AD=CF,
∴四边形ADFC是平行四边形,
∵∠ADF=90°,
∴四边形ADFC是矩形,
∴HE=AD=33cm,
∵BE=90cm,
∴BH=57cm,
在Rt△HCB中,sin∠BCH=![]() =
=![]() =
=![]() =0.95,
=0.95,
∴∠ACB=72°.
(2)如图所示,B'E'=96.8cm,设B'E'与AC交于点H',则有B'H'∥BH,
∴△B'H'C∽△BHC,
∴![]() =
=![]() .
.
即![]() =
=![]() ,
,
∴B'C=67cm.
故BB'=B'C﹣BC=67﹣60=7(cm).
∴车架中立管BC拉长的长度BB'应是7cm.



 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高1元其销售量就减少20件.
![]() 问应将每件售价定为多少元时,才能使每天利润为640元?
问应将每件售价定为多少元时,才能使每天利润为640元?
![]() 当售价定为多少时,获得最大利润;最大利润是多少?
当售价定为多少时,获得最大利润;最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
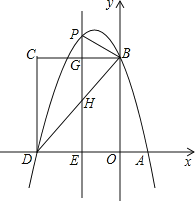
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,则当天该水果的销售量 千克.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
(3)当售价定为多少元时,当天销售这种水果获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
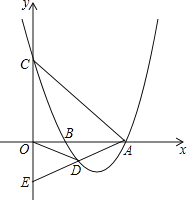
【题目】如图,抛物线y=mx2-16mx+48m(m>0)与x轴交于A、B两点(点B在点A左侧),与y轴交于点C,点D是抛物线上的一个动点,且位于第四象限,连接OD、BD、AC、AD,延长AD交y轴于点E.
(1)若△OAC为等腰直角三角形,求m的值.
(2)若对任意m>0,C、E两点总关于原点对称,求点D的坐标(用含m的式子表示).
(3)当点D运动到某一位置时,恰好使得∠ODB=∠OAD,且点D为线段AE的中点,此时对于该抛物线上任意一点P(x0,y0)总有n≥-4![]() my02-12
my02-12![]() y0-50成立,求实数n的最小值.
y0-50成立,求实数n的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解方程:x2﹣2x﹣3=0;
(2)如图,正方形ABCD中,点E,F,C分别在AB,BC,CD上,且∠EFG=90°;求证:△EBF∽△FCG.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0,a、b、c为常数)上部分点的横坐标x,纵坐标y的对应值如下表:
x | …… | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | …… |
y | …… |
| 4 |
| 4 | m | 0 | …… |
则下列结论中:①抛物线的对称轴为直线x=﹣1;②m=![]() ;③当﹣4<x<2时,y<0;④方程ax2+bx+c﹣4=0的两根分别是x1=﹣2,x2=0,其中正确的个数有( )
;③当﹣4<x<2时,y<0;④方程ax2+bx+c﹣4=0的两根分别是x1=﹣2,x2=0,其中正确的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,1),B(1,-2),C(3,-1),P(m,n)是△ABC的边AB上一点.

(1)画出△A1B1C1,使△A1B1C1与△ABC关于点O成中心对称,并写出点A、P的对应点A1、P1的坐标.
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出将△A1B1C1放大后的△A2B2C2,并分别写出点A1、P1的对应点A2、P2的坐标.
(3)求sin∠B2A2C2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,C(0,4),A为x轴上一动点,连接AC,将AC绕A点顺时针旋转90°得到AB,当点A在x轴上运动时,OB+BC的最小值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com