
【题目】(1)解方程:x2﹣2x﹣3=0;
(2)如图,正方形ABCD中,点E,F,C分别在AB,BC,CD上,且∠EFG=90°;求证:△EBF∽△FCG.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
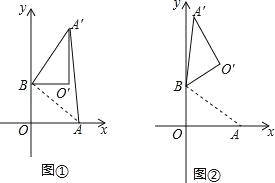
【题目】在平面直角坐标系中,O 为原点,点 A(4,0),点 B(0,3),把△ABO 绕点 B 逆时针旋转,得△A′BO′,点 A、O 旋转后的对应点为 A′、O′,记旋转角为ɑ.
(1)如图 1,若ɑ=90°,求 AA′的长;
(2)如图 2,若ɑ=120°,求点 O′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有三个完全相同的小球,分别标有数字2,3,4.从袋子中随机取出一个小球,用小球上的数字作为十位数字,然后放回,再取出一个小球,用小球上的数字作为个位数字,这样组成一个两位数,请用列表法或画树状图的方法完成下列问题.
(1)按这种方法组成两位数45是_____事件,填(“不可能”、“随机”、“必然”)
(2)组成的两位数能被3整除的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自行车因其便捷环保深受人们喜爱,成为日常短途代步与健身运动首选.如图1是某品牌自行车的实物图,图2是它的简化示意图.经测量,车轮的直径为66cm,车座B到地面的距离BE为90cm,中轴轴心C到地面的距离CF为33cm,车架中立管BC的长为60cm,后轮切地面L于点D.(参考数据:sin72≈0.95,cos18°≈0.95,tan43.5°≈0.9 5)
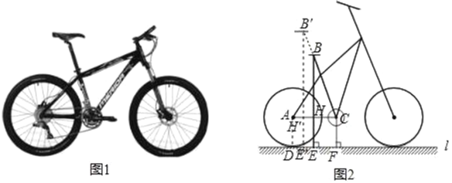
(1)求∠ACB的大小(精确到1°)
(2)如果希望车座B到地面的距离B'E′为96.8cm,车架中立管BC拉长的长度BB′应是多少?(结果取整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,抛物线y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,直线l经过B、C两点,点M从点A出发以每秒1个单位长度的速度向终点B运动,连接CM,将线段MC绕点M顺时针旋转90°得到线段MD,连接CD、BD.设点M运动的时间为t(t>0),请解答下列问题:
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,直线l经过B、C两点,点M从点A出发以每秒1个单位长度的速度向终点B运动,连接CM,将线段MC绕点M顺时针旋转90°得到线段MD,连接CD、BD.设点M运动的时间为t(t>0),请解答下列问题:

(1)求点A的坐标与直线l的表达式;
(2)①请直接写出点D的坐标(用含t的式子表示),并求点D落在直线l上时t的值;
②求点M运动的过程中线段CD长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
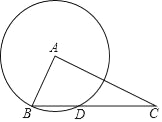
【题目】如图,已知Rt△ABC,∠BAC=90°,BC=5,AC=2![]() ,以A为圆心、AB为半径画圆,与边BC交于另一点D.
,以A为圆心、AB为半径画圆,与边BC交于另一点D.
(1)求BD的长;
(2)连接AD,求∠DAC的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (其中
(其中![]() 、
、![]() 为常数且
为常数且![]() )与
)与![]() 轴交于
轴交于![]() 和
和![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)当![]() 时,求抛物线的对称轴方程及顶点坐标;
时,求抛物线的对称轴方程及顶点坐标;
(2)填空:![]() __________,点
__________,点![]() 的坐标为____________.(以上结果均用含
的坐标为____________.(以上结果均用含![]() 的式子表示);
的式子表示);
(3)连接![]() ,线段
,线段![]() 的垂直平分线交抛物线的对称轴于点
的垂直平分线交抛物线的对称轴于点![]() ,
,![]() 轴上存在一点
轴上存在一点![]() (异于点
(异于点![]() )使得
)使得![]() .
.
①求点![]() 的坐标;
的坐标;
②点![]() 关于抛物线对称轴的对称点为点
关于抛物线对称轴的对称点为点![]() ,试求
,试求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2﹣2ax﹣3(a≠0)与x轴交于A,B两点(点A在点B左侧).

(1)求抛物线的对称轴;
(2)若AB=4,求该抛物线的解析式;
(3)若AB≤4,直接写出a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com