
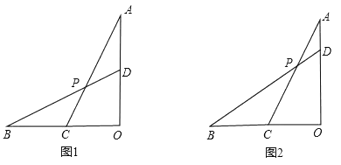
【题目】已知线段![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上一点,连接
上一点,连接![]() 交于
交于![]() 点.
点.
(1)如图1,当![]() 且
且![]() 为
为![]() 中点时,求
中点时,求![]() 的值.
的值.
(2)如图2,当![]() ,
,![]() =
=![]() 时,求tan∠
时,求tan∠![]() 的值.
的值.
【答案】(1)![]() ;(2)tan∠BPC=
;(2)tan∠BPC=![]() .
.
【解析】
(1)连结AB、CD,首先证明点P为△OAB的重心,得到![]() ,然后利用勾股定理求出AP即可;
,然后利用勾股定理求出AP即可;
(2)延长AC至点H,使CH=CA,连接BH,易证△BCH≌△OCA,得到BH=OA,∠CBH=∠O,然后设AD=t,OD=3t,则BH=OA=OB=4t,根据△HBP∽△ADP列比例式求出BP=4t,得到BH=BP,然后根据tan∠BPC=tan∠H求解即可.
解:(1)连结AB、CD,
∵C、D分别为OB、OA的中点,
∴AC、BD为△OAB边OB、OA的中线,
∴点P为△OAB的重心,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴在Rt△AOC中,![]() ,
,
∴![]() ;
;
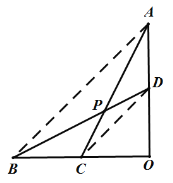
(2)延长AC至点H,使CH=CA,连接BH,
∵C是OB的中点,
易得△BCH≌△OCA(SAS),
∴BH=OA,∠CBH=∠O,
由![]() ,设AD=t,OD=3t,则BH=OA=OB=4t,
,设AD=t,OD=3t,则BH=OA=OB=4t,
在Rt△BOD中,BD=![]() ,
,
∵∠CBH=∠O,
∴OA//BH,
∴△HBP∽△ADP,
∴![]() ,
,
∴BP=4PD=![]() BD=4t,
BD=4t,
∴BH=BP,
∴∠BPC=∠H,
∴tan∠BPC=tan∠H=![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,sinA=![]() ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在△ABC中,AB=AC,∠BAC=120°,BC=12,则AB的长度为 ;
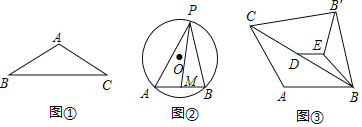
(2)如图②,⊙O的半径为16,弦AB=16,M是AB的中点,P是⊙O上一动点,求PM的最大值;
(3)如图③,在△ABC中AB=AC=8,∠CAB=120°,D是BC的中点,E是平面内一点,且ED=2,连接BE,将EB绕点E逆时针旋转120°,得到EB′,连接CB′、BB′,四边形ABB′C的面积是否存在最大值,若存在,求出四边ABB′C的面积的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线yn=﹣(x﹣an)2+bn,(n为正整数,且0≤a1<a2<…≤an)与x轴的交点为
A(0,0)和An(n,0),n=Cn﹣1+2,当n=1时,第1条抛物线y1=﹣(x﹣a1)2+b1与x轴的交点为A(0,0)和A1(2,0),其他依此类推.
(1)求a1,b1的值及抛物线y2的解析式.
(2)抛物线的顶点B坐标为(_____,______);依此类推,第n+1条抛物线yn+1的顶点Bn+1坐标为(____,_____)所有抛物线的顶点坐标满足的函数关系式是______.
(3)探究下结论:
①是否存在抛物线yn,使得△AAnBn为等腰直角三角形?若存在请求出抛物线的表达式;若不存在,请说明理由.
②若直线x=m(m>0)与抛物线yn分别交于C1,C2,…,Cn则线段C1C2,C2C3,…,Cn﹣1Cn的长有何规律?请用含有m的代数式表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,则当天该水果的销售量 千克.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
(3)当售价定为多少元时,当天销售这种水果获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,△ABC为等边三角形,其中点A、B、C的坐标分别为(﹣3,﹣1)、(﹣3,﹣3)、(﹣3+![]() ,﹣2).现以y轴为对称轴作△ABC的对称图形,得△A1B1C1,再以x轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.
,﹣2).现以y轴为对称轴作△ABC的对称图形,得△A1B1C1,再以x轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.
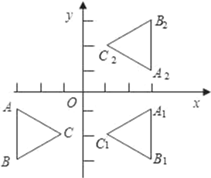
①直接写出点C1的坐标 ,点C2的坐标 ;
②能否通过一次旋转将△ABC旋转到△A2B2C2的位置?你若认为能,请作出肯定的回答,并直接写出所旋转的度数;你若认为不能,请作出否定的回答(不必说明理由);
③设当△ABC的位置发生变化时,△A2B2C2、△A1B1C1、△ABC之间的对称关系始终保持不变,当△ABC向上平移多少个单位时,△A1B1C1与△A2B2C2完全重合?并直接写出此时点C的坐标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解方程:x2﹣2x﹣3=0;
(2)如图,正方形ABCD中,点E,F,C分别在AB,BC,CD上,且∠EFG=90°;求证:△EBF∽△FCG.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+6与反比例数y=![]() (x>0)的图象交于点A(1,m),与x轴交于点B,与y轴交于点D.
(x>0)的图象交于点A(1,m),与x轴交于点B,与y轴交于点D.
(1)求m的值和反比例函数的表达式;
(2)观察图像,直接写出不等式2x+6-![]() >0的解集
>0的解集
(3)在反比例函数图像的第一象限上有一动点M,当S△BOM<S△BOD 时,直接写出点M纵坐标的的取值范围。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com