
【题目】已知抛物线yn=﹣(x﹣an)2+bn,(n为正整数,且0≤a1<a2<…≤an)与x轴的交点为
A(0,0)和An(n,0),n=Cn﹣1+2,当n=1时,第1条抛物线y1=﹣(x﹣a1)2+b1与x轴的交点为A(0,0)和A1(2,0),其他依此类推.
(1)求a1,b1的值及抛物线y2的解析式.
(2)抛物线的顶点B坐标为(_____,______);依此类推,第n+1条抛物线yn+1的顶点Bn+1坐标为(____,_____)所有抛物线的顶点坐标满足的函数关系式是______.
(3)探究下结论:
①是否存在抛物线yn,使得△AAnBn为等腰直角三角形?若存在请求出抛物线的表达式;若不存在,请说明理由.
②若直线x=m(m>0)与抛物线yn分别交于C1,C2,…,Cn则线段C1C2,C2C3,…,Cn﹣1Cn的长有何规律?请用含有m的代数式表示.
【答案】(1)a1=1,a2=1,y2=﹣(x﹣2)2+4;(2)n,n2;n+1,(n+1)2;y=x2;(3)①存在,y=﹣(x﹣1)2+1;②Cn﹣1Cn=2m.
【解析】
(1)A1(2,0),则C1=2,则C2=2+2=4,将点A、A1的坐标代入抛物线表达式得: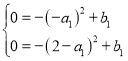 ,解得:
,解得:![]() ,则点A2(4,0),将点A、A2的坐标代入抛物线表达式,同理可得:a2=2,b2=4,即可求解;
,则点A2(4,0),将点A、A2的坐标代入抛物线表达式,同理可得:a2=2,b2=4,即可求解;
(2)同理可得:a3=3,b3=9,故点B的坐标为(n,n2),以此推出:点B[(n+1,(n+1)2],故所有抛物线的顶点坐标满足的函数关系式是:y=x2,即可求解;
(3)①△AAnBn为等腰直角三角形,则AAn2=2ABn2,即(2n)2=2(n2+n4),即可求解;
②yCn﹣1=﹣(m﹣n+1)2+(n﹣1)2,yCn=﹣(m﹣n)2+n2,Cn﹣1n=yCn﹣yCn﹣1,即可求解.
解:(1)A1(2,0),则C1=2,则C2=2+2=4,
将点A、A1的坐标代入抛物线表达式得: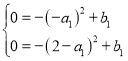 ,解得:
,解得:![]() ,
,
则点A2(4,0),将点A、A2的坐标代入抛物线表达式,同理可得:a2=2,b2=4;
故y2=﹣(x﹣a2)2+b2=﹣(x﹣2)2+4;
(2)同理可得:a3=3,b3=9,故点B的坐标为(n,n2),
以此推出:点B[(n+1,(n+1)2],
故所有抛物线的顶点坐标满足的函数关系式是:y=x2,
故答案为:(n,n2);[(n+1,(n+1)2];y=x2;
(3)①存在,理由:
点A(0,0),点An(2n,0)、点Bn(n,n2),
△AAnBn为等腰直角三角形,则AAn2=2ABn2,
即(2n)2=2(n2+n4),解得:n=1(不合题意的值已舍去),
抛物线的表达式为:y=﹣(x﹣1)2+1;
②yCn﹣1=﹣(m﹣n+1)2+(n﹣1)2,
yCn=﹣(m﹣n)2+n2,
Cn﹣1Cn=yCn﹣yCn﹣1=﹣(m﹣n)2+n2+(m﹣n+1)2﹣(n﹣1)2=2m.


科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD内接于⊙O,AB=AC,过点A作AE∥BD交CD的延长线于点E.
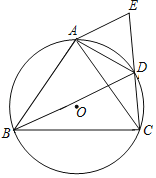
(1)求证:AE=DE;
(2)若∠BCD﹣∠CBD=60°,求∠ABD的度数;
(3)在(2)的条件下,若BD=21,CD=9,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市面上贩售的防晒产品标有防晒指数![]() ,而其对抗紫外线的防护率算法为:防护率
,而其对抗紫外线的防护率算法为:防护率![]() ,其中
,其中![]() .
.
请回答下列问题:
(1)厂商宣称开发出防护率![]() 的产品,请问该产品的
的产品,请问该产品的![]() 应标示为多少?
应标示为多少?
(2)某防晒产品文宣内容如图所示.
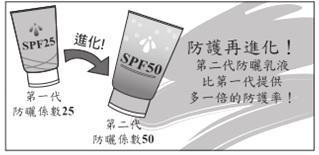
请根据![]() 与防护率的转换公式,判断此文宣内容是否合理,并详细解释或完整写出你的理由.
与防护率的转换公式,判断此文宣内容是否合理,并详细解释或完整写出你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:河上有一座抛物线形桥洞,已知桥下的水面离桥拱顶部3m时,水面宽AB=6m,建立如图所示的坐标系.
(1)当水位上升0.5m时,求水面宽度CD为多少米?(结果可保留根号)
(2)有一艘游船它的左右两边缘最宽处有一个长方体形状的遮阳棚,此船正对着桥洞在上述河流中航行,若这船宽(最大宽度)2米,从水面到棚顶高度为1.8米.问这艘船能否从桥下洞通过?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有三个完全相同的小球,分别标有数字2,3,4.从袋子中随机取出一个小球,用小球上的数字作为十位数字,然后放回,再取出一个小球,用小球上的数字作为个位数字,这样组成一个两位数,请用列表法或画树状图的方法完成下列问题.
(1)按这种方法组成两位数45是_____事件,填(“不可能”、“随机”、“必然”)
(2)组成的两位数能被3整除的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在直角坐标系中画出二次函数y=![]() x2﹣x﹣
x2﹣x﹣![]() 的图象.
的图象.
(2)若将y=![]() x2﹣x﹣
x2﹣x﹣![]() 图象沿x轴向左平移2个单位,请写出平移后图象所对应的函数关系式.
图象沿x轴向左平移2个单位,请写出平移后图象所对应的函数关系式.
(3)根据图象,写出当y>0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,抛物线y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,直线l经过B、C两点,点M从点A出发以每秒1个单位长度的速度向终点B运动,连接CM,将线段MC绕点M顺时针旋转90°得到线段MD,连接CD、BD.设点M运动的时间为t(t>0),请解答下列问题:
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,直线l经过B、C两点,点M从点A出发以每秒1个单位长度的速度向终点B运动,连接CM,将线段MC绕点M顺时针旋转90°得到线段MD,连接CD、BD.设点M运动的时间为t(t>0),请解答下列问题:

(1)求点A的坐标与直线l的表达式;
(2)①请直接写出点D的坐标(用含t的式子表示),并求点D落在直线l上时t的值;
②求点M运动的过程中线段CD长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2﹣(m﹣3)x﹣m2=0.
(1)证明:方程总有两个不相等的实数根;
(2)设这个方程的两个实数根为x1,x2,且|x1|=|x2|﹣2,求m的值及方程的根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com