
【题目】已知:如图,四边形ABCD内接于⊙O,AB=AC,过点A作AE∥BD交CD的延长线于点E.
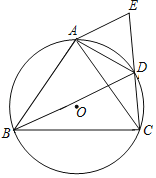
(1)求证:AE=DE;
(2)若∠BCD﹣∠CBD=60°,求∠ABD的度数;
(3)在(2)的条件下,若BD=21,CD=9,求AE的长.
【答案】(1)见解析;(2)30°;(3)AE的长为![]()
【解析】
(1)根据题意得∠1=∠ABC,∠2=∠3,证明得到∠1=∠2,即可证明AE=DE;
(2)根据题意得∠5=∠6,∠ABC=∠4,则∠BCD=∠4+∠6=∠5+∠CBD+∠6,再由∠BCD﹣∠CBD=60°,即可求出∠ABD的度数;
(3)作AM⊥BD于M,AN⊥EC于N,先证明△ADM≌△AND,求出BM和AM的值,设AE=x,则DE=x,NE=x﹣6,在Rt△ANE中,根据勾股定理建立方程解出即可.
(1)证明:如图1中,
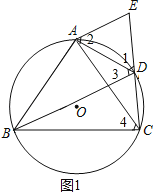
∵四边形ABCD内接于⊙O,
∴∠1=∠ABC,
∵AE∥BD,
∴∠2=∠3,
∵∠3=∠4,
∵AB=AC,
∴∠ABC=∠4,
∴∠1=∠2,
∴AE=AD.
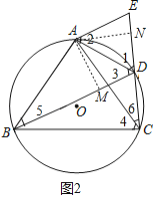
(2)解:如图2中,
∵∠5=∠6,∠ABC=∠4,
∴∠BCD=∠4+∠6=∠5+∠CBD+∠6,
∵∠BCD﹣∠CBD=60°,
∴∠5=∠6=30°.
(3)解:如图2中,作AM⊥BD于M,AN⊥EC于N,
∵∠5=∠6,AB=AC,∠AMB=∠ANC=90°,
∴△AMB≌△ANC(AAS),
∴AM=AN,BM=CN,
∵∠3=∠1,AD=AD,∠AND=∠AMD=90°,
∴△ADM≌△ADN(AAS),
∴DN=DM,
∴DM=DN=![]() (BD﹣CD)=6,
(BD﹣CD)=6,
在Rt△AMB中,∵∠5=30°,BM=15,
∴BM2+AM2=AB2,AB=2AM,AN=AM=5![]() ,
,
设AE=x,则DE=x,NE=x﹣6,
在Rt△ANE中,∵AN2+NE2=AE2,
∴(5![]() )2+(x﹣6)2=x2,
)2+(x﹣6)2=x2,
∴x=![]() ,
,
∴AE的长为![]() .
.


科目:初中数学 来源: 题型:
【题目】基础知识考查:
(1)一次函数表达式 ,当k>0,b>0时,图像经过 象限;当k>0,b<0时,图像经过 象限;当k<0,b>0时,图像经过 象限;当k<0,b<0时,图像经过 象限.特别当b=0时,图像经过 ,称为 函数.
(2)反比例函数三种表达方式分别为: 、 、 反比例函数的图像称为 ,当k>0时,图像在 和 象限,y随x的增大而 ;当k<0时,图像在 和 象限,y随x的增大而 .
(3)特殊三角函数值:
0° | 30° | 45° | 60° | 90° | |
sinA | |||||
cosA | |||||
tanA | |||||
cotA |
(4)二次函数表达式:
①一般式: ;
②顶点式: ; ; ;
.
③交点式(点式): ;
④对称轴公式: 顶点坐标公式: .
⑤二次函数图像称为 ,当a>0时,图像开口向 ;当a<0时,图像开口向 .c>0时,图像和 轴正半轴相交,c<0时,图像和 轴负半轴相交.
查看答案和解析>>
科目:初中数学 来源: 题型:
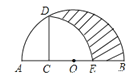
【题目】如图,AB为半圆O的直径,C为AO的中点,CD⊥AB交半圆于点D,以C为圆心,CD为半径画弧DE交AB于E点,若AB=4cm,则图中阴影部分的面积为__________cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,已知点P(m﹣1,n2),Q(m,n﹣1),其中m<0,则下列函数的图象可能同时经过P,Q两点的是( )
A.y=2x+bB.y=﹣x2+2x+c
C.y=ax+2 (a>0)D.y=ax2﹣2ax+c(a>0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 (1),已知△ABC是等边三角形,以BC为直径的⊙O交AB、AC于D、E.求证:

(1)△DOE是等边三角形.
(2)如图(2),若∠A=60°,AB≠AC, 则(1)中结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,sinA=![]() ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①abc<0;②2a+b=0; ③b2﹣4ac<0; ④9a+3b+c>0.其中正确的结论有____________( 填序号 )
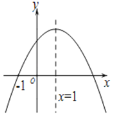
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线yn=﹣(x﹣an)2+bn,(n为正整数,且0≤a1<a2<…≤an)与x轴的交点为
A(0,0)和An(n,0),n=Cn﹣1+2,当n=1时,第1条抛物线y1=﹣(x﹣a1)2+b1与x轴的交点为A(0,0)和A1(2,0),其他依此类推.
(1)求a1,b1的值及抛物线y2的解析式.
(2)抛物线的顶点B坐标为(_____,______);依此类推,第n+1条抛物线yn+1的顶点Bn+1坐标为(____,_____)所有抛物线的顶点坐标满足的函数关系式是______.
(3)探究下结论:
①是否存在抛物线yn,使得△AAnBn为等腰直角三角形?若存在请求出抛物线的表达式;若不存在,请说明理由.
②若直线x=m(m>0)与抛物线yn分别交于C1,C2,…,Cn则线段C1C2,C2C3,…,Cn﹣1Cn的长有何规律?请用含有m的代数式表示.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com