
����Ŀ����ˮ������������ijˮ���깺��һ����ˮ��������Ϊ20Ԫ/ǧ�ˣ��ۼ۲�����20Ԫ/ǧ�ˣ��Ҳ�����32Ԫ/ǧ�ˣ�����������������ָ�ˮ��һ���������y��ǧ�ˣ��������ۼ�x��Ԫ/ǧ�ˣ��������±���ʾ��һ�κ�����ϵ��
������y��ǧ�ˣ� | �� | 34.8 | 32 | 29.6 | 28 | �� |
�ۼ�x��Ԫ/ǧ�ˣ� | �� | 22.6 | 24 | 25.2 | 26 | �� |
��1��ij������ˮ�����ۼ�Ϊ23.5Ԫ/ǧ�ˣ������ˮ���������� ǧ�ˣ�
��2�����ij����������ˮ������150Ԫ����ô����ˮ�����ۼ�Ϊ����Ԫ��
��3�����ۼ۶�Ϊ����Ԫʱ��������������ˮ�����������������Ƕ��٣�
���𰸡���1��33ǧ�ˣ���2���ۼ�Ϊ25Ԫ����3���ۼ۶�Ϊ30Ԫʱ����������������Ϊ200Ԫ
��������
��1�����ݱ����ڵ����ݣ����ô���ϵ���������y��x֮��ĺ�����ϵʽ���ٴ���x=23.5����������ۣ�
��2������������=ÿǧ���������������������ɵó�����x��һԪ���η��̣���֮ȡ���Сֵ���ɵó����ۣ�
��3������������Եõ��������x�ĺ�����ϵʽ��Ȼ�����ö��κ��������ʼ��ɽ��
�⣺��1����y��x֮��ĺ�����ϵʽΪy=kx+b��
����26��28������24��32������y=kx+b��![]() ����ã�
����ã�![]() ��
��
��y��x֮��ĺ�����ϵʽΪy=-2x+80��
��x=23.5ʱ��y=-2x+80=33��
�𣺵����ˮ����������Ϊ33ǧ�ˣ�
��2������������x��20������2x+80��=150
��ã�x1=35 x2=25
�֡�20��x��32
��x=25��
�����ij����������ˮ������150Ԫ����ô����ˮ�����ۼ�Ϊ25Ԫ��
��3�� ��������ΪWԪ����
W=��x��20������2x+80��
=��2x2+120x��1600
=��2��x��30��2+200
��a=��2��0
�൱�ۼ۶�Ϊ30Ԫʱ����������������Ϊ200Ԫ


 ��һ����ͬ���ɽ�����ϵ�д�
��һ����ͬ���ɽ�����ϵ�д� ������Ӧ���ϵ�д�
������Ӧ���ϵ�д� ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
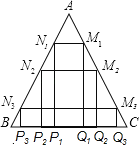
����Ŀ����ͼ������ABC�У�AB��AC��![]() ��BC��2���ֱַ�������ABC���ڽӾ���P1Q1M1N1��P2Q2M2N2��P3Q3M3N3�����������ڽӾ��ε��ܳ��ֱ�Ϊc1��c2��c3����c1+c2+c3��ֵ�ǣ�������
��BC��2���ֱַ�������ABC���ڽӾ���P1Q1M1N1��P2Q2M2N2��P3Q3M3N3�����������ڽӾ��ε��ܳ��ֱ�Ϊc1��c2��c3����c1+c2+c3��ֵ�ǣ�������
A. 6B. ![]() C. 12D.
C. 12D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
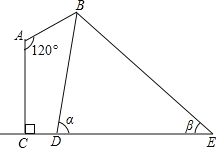
����Ŀ����ͼ��ij·����Ǧ�����ڵ�ʾ��ͼ������AC�ĸ�Ϊ15.25�ף��Ƹ�AB�����AC�ļнǡ�A��120����·�Ʋ����ε��֣��ڵ����ϵ���������DE��Ϊ22�ף���D��E�������·��B�����Ƿֱ�Ϊ����������tan����8��tan����![]() ����Ƹ�AB�ij��ȣ�
����Ƹ�AB�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ĵ�����װ��������ȫ��ͬ��С�ֱ��������2��3��4.�Ӵ��������ȡ��һ��С����С���ϵ�������Ϊʮλ���֣�Ȼ��Żأ���ȡ��һ��С����С���ϵ�������Ϊ��λ���֣��������һ����λ���������б�������״ͼ�ķ��������������.
(1)�����ַ��������λ��45��_____�¼�����(�������������������������Ȼ��)
(2)��ɵ���λ���ܱ�3�����ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
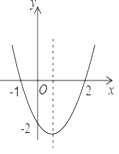
����Ŀ����ͼ�����κ���y��ax2+bx+c��ͼ����ͼ��ʾ�����½��ۣ���abc��0�� ��b2-4ac��0 �� ��2a+b��0 ����a+b+c��0��������ȷ�ĸ����� ��
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�߶�![]() ��
��![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() Ϊ
Ϊ![]() ��һ�㣬����
��һ�㣬����![]() ����
����![]() ��.
��.
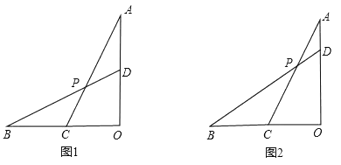
(1)��ͼ1����![]() ��
��![]() Ϊ
Ϊ![]() �е�ʱ����
�е�ʱ����![]() ��ֵ.
��ֵ.
(2)��ͼ2����![]() ��
��![]() =
=![]() ʱ����tan��
ʱ����tan��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����г������ݻ�����������ϲ������Ϊ�ճ���;�����뽡���˶���ѡ����ͼ1��ijƷ�����г���ʵ��ͼ��ͼ2�����ļ�ʾ��ͼ�������������ֵ�ֱ��Ϊ66cm������B������ľ���BEΪ90cm����������C������ľ���CFΪ33cm������������BC�ij�Ϊ60cm�������е���L�ڵ�D�����ο����ݣ�sin72��0.95��cos18���0.95��tan43.5���0.9 5��
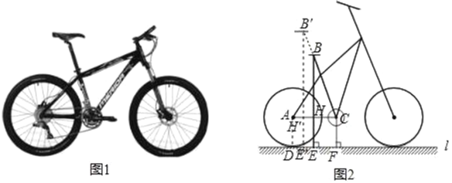
��1�����ACB�Ĵ�С����ȷ��1�㣩
��2�����ϣ������B������ľ���B'E��Ϊ96.8cm������������BC�����ij���BB��Ӧ�Ƕ��٣������ȡ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪Rt��ABC����BAC��90����BC��5��AC��2![]() ����AΪԲ�ġ�ABΪ�뾶��Բ�����BC������һ��D��
����AΪԲ�ġ�ABΪ�뾶��Բ�����BC������һ��D��
��1����BD�ij���
��2������AD�����DAC������ֵ��
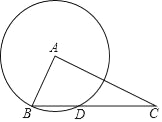
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ԲO�İ뾶Ϊ![]() ����M������Ϊ��m��3��������ԲO�ϴ���һ��N, ��M��NΪ�����ε��������㣬�������εı߾������������ᴹֱ����m����СֵΪ_________
����M������Ϊ��m��3��������ԲO�ϴ���һ��N, ��M��NΪ�����ε��������㣬�������εı߾������������ᴹֱ����m����СֵΪ_________
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com