
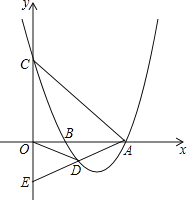
【题目】如图,抛物线y=mx2-16mx+48m(m>0)与x轴交于A、B两点(点B在点A左侧),与y轴交于点C,点D是抛物线上的一个动点,且位于第四象限,连接OD、BD、AC、AD,延长AD交y轴于点E.
(1)若△OAC为等腰直角三角形,求m的值.
(2)若对任意m>0,C、E两点总关于原点对称,求点D的坐标(用含m的式子表示).
(3)当点D运动到某一位置时,恰好使得∠ODB=∠OAD,且点D为线段AE的中点,此时对于该抛物线上任意一点P(x0,y0)总有n≥-4![]() my02-12
my02-12![]() y0-50成立,求实数n的最小值.
y0-50成立,求实数n的最小值.
【答案】(1)m=![]() ;(2)点D的坐标为(8,-16m);(3)实数n的最小值为
;(2)点D的坐标为(8,-16m);(3)实数n的最小值为![]()
【解析】
(1)根据y=mx2-16mx+48m=m(x-4)(x-12),可得A(12,0),C(0,48m),再根据OA=OC,即可得到12=48m,进而得出m的值;
(2)根据C、E两点总关于原点对称,得到E(0,48m),根据E(0,48m),A(12,0)可得直线AE的解析式,最后解方程组即可得到直线AE与抛物线的交点D的坐标;
(3)根据△ODB∽△OAD,可得OD=4![]() ,进而得到D(6,2
,进而得到D(6,2![]() ),代入抛物线y=mx216mx+48m,求出m可得抛物线解析式,再根据点P(x0,y0)为抛物线上任意一点,即可得出y0≥
),代入抛物线y=mx216mx+48m,求出m可得抛物线解析式,再根据点P(x0,y0)为抛物线上任意一点,即可得出y0≥![]() ,令t=-4
,令t=-4![]() my02-12
my02-12![]() y0-50,求出t最大值=2(
y0-50,求出t最大值=2(![]() )2+4=
)2+4=![]() ,即可得实数n的最小值为
,即可得实数n的最小值为![]() .
.
解:(1)令y=mx2-16mx+48m=m(x-4)(x-12)=0,
则x1=12,x2=4,
∴A(12,0),即OA=12,
又∵C(0,48m),
∴当△OAC为等腰直角三角形时,OA=OC,即12=48m,
∴m=![]() ;.
;.
(2)由(1)可知点C(0,48m),
∵对任意m>0,C、E两点总关于原点对称,
∴必有E(0,-48m),
设直线AE的解析式为y=kx+b(k≠0),
将E(0,-48m),A(12,0)代入,可得![]() ,解得
,解得![]() ,
,
∴直线AE的解析式为y=4mx-48m,
∵点D为直线AE与抛物线的交点,
∴解方程组![]() ,得
,得![]() 或
或![]() (舍去),
(舍去),
∴点D的坐标为(8,-16m);
(3)当∠ODB=∠OAD,∠DOB=∠AOD时,△ODB∽△OAD,
∴![]() ,
,
∴OD2=OA×OB=12×4=48,
∴OD=4![]() ,
,
又∵点D为线段AE的中点,
∴AE=2OD=8![]() ,
,
又∵OA=12,
∴OE=![]() =4
=4![]() ,
,
∴D(6,-2![]() ),
),
把D(6,-2![]() )代入抛物线y=mx2-16mx+48m,可得-2
)代入抛物线y=mx2-16mx+48m,可得-2![]() =36m-96m+48m,
=36m-96m+48m,
解得:m=![]() ,
,
∴抛物线的解析式为y=![]() (x-4)(x-12),即y=
(x-4)(x-12),即y=![]() (x-8)2-
(x-8)2-![]() ,
,
∵点P(x0,y0)为抛物线上任意一点,
∴y0≥-![]() ,
,
令t=-4![]() my02-12
my02-12![]() y0-50=-2y02-12
y0-50=-2y02-12![]() y0-50=-2(y0+3
y0-50=-2(y0+3![]() )2+4,
)2+4,
则当y0≥-![]() 时,t最大值=-2(-
时,t最大值=-2(-![]() +3
+3![]() )2+4=
)2+4=![]() ,
,
若要使n≥-4![]() my02-12
my02-12![]() y0-50成立,则n≥
y0-50成立,则n≥![]() ,
,
∴n≥![]() ,
,
∴实数n的最小值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某区各街道居民积极响应“创文明社区”活动,据了解,某街道居民人口共有7.5万人,街道划分为A,B两个社区,B社区居民人口数量不超过A社区居民人口数量的2倍.
(1)求A社区居民人口至少有多少万人?
(2)街道工作人员调查A,B两个社区居民对“社会主义核心价值观”知晓情况发现:A社区有1.2万人知晓,B社区有1万人知晓,为了提高知晓率,街道工作人员用了两个月的时间加强宣传,A社区的知晓人数平均月增长率为m%,B社区的知晓人数第一个月增长了m%,第二个月增长了2m%,两个月后,街道居民的知晓率达到76%,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
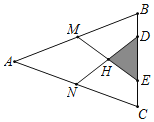
【题目】在△ABC中,AB=AC=13cm,BC=10cm,M、N分别是AB、AC的中点,D、E在BC上,且DE=5cm,连结DN、ME交于H,则△HDE的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
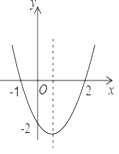
【题目】如图,二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0; ②b2-4ac<0 ; ③2a+b>0 ;④a+b+c>0,其中正确的个数( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
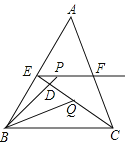
【题目】如图,在△ABC中,BC=6,E,F分别是AB,AC的中点,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于点Q,当CQ=QE时,EP+BP的值为( ).
A.6B.9C.12D.18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自行车因其便捷环保深受人们喜爱,成为日常短途代步与健身运动首选.如图1是某品牌自行车的实物图,图2是它的简化示意图.经测量,车轮的直径为66cm,车座B到地面的距离BE为90cm,中轴轴心C到地面的距离CF为33cm,车架中立管BC的长为60cm,后轮切地面L于点D.(参考数据:sin72≈0.95,cos18°≈0.95,tan43.5°≈0.9 5)
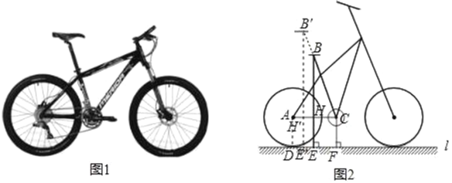
(1)求∠ACB的大小(精确到1°)
(2)如果希望车座B到地面的距离B'E′为96.8cm,车架中立管BC拉长的长度BB′应是多少?(结果取整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在小水池旁有一盏路灯,已知支架AB的长是0.8m,A端到地面的距离AC是4m,支架AB与灯柱AC的夹角为65°.小明在水池的外沿D测得支架B端的仰角是45°,在水池的内沿E测得支架A端的仰角是50°(点C、E、D在同一直线上),求小水池的宽DE.(结果精确到0.1m)(sin65°≈0.9,cos65°≈0.4,tan50°≈1.2)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣4和y=﹣ax2+4都经过x轴上的A、B两点,两条抛物线的顶点分别为C、D.当四边形ACBD的面积为40时,a的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某店代理某品牌商品的销售.已知该品牌商品进价每件40元,日销售y(件)与销售价x(元/件)之间的关系如图所示(实线),付员工的工资每人每天100元,每天还应支付其它费用150元.

(1)求日销售y(件)与销售价x(元/件)之间的函数关系式;
(2)该店员工人共3人,若某天收支恰好平衡(收入=支出),求当天的销售价是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com