
【题目】某区各街道居民积极响应“创文明社区”活动,据了解,某街道居民人口共有7.5万人,街道划分为A,B两个社区,B社区居民人口数量不超过A社区居民人口数量的2倍.
(1)求A社区居民人口至少有多少万人?
(2)街道工作人员调查A,B两个社区居民对“社会主义核心价值观”知晓情况发现:A社区有1.2万人知晓,B社区有1万人知晓,为了提高知晓率,街道工作人员用了两个月的时间加强宣传,A社区的知晓人数平均月增长率为m%,B社区的知晓人数第一个月增长了m%,第二个月增长了2m%,两个月后,街道居民的知晓率达到76%,求m的值.
【答案】(1) A社区居民人口至少有2.5万人;(2)50.
【解析】
(1)设A社区居民人口有x万人,根据“B社区居民人口数量不超过A社区居民人口数量的2倍”列出不等式求解即可;
(2)A社区的知晓人数+B社区的知晓人数=7.5×76%,据此列出关于m的方程并解答.
解:(1)设A社区居民人口有x万人,则B社区有(7.5x)万人,
依题意得:7.5x≤2x,
解得x≥2.5.
即A社区居民人口至少有2.5万人;
(2)依题意得:1.2(1+m%)2+1×(1+m%)×(1+2m%)=7.5×76%,
设m%=a,方程可化为:1.2(1+a)2+(1+a)(1+2a)=5.7,
化简得:32a2+54a35=0,
解得a=0.5或a=![]() (舍),
(舍),
∴m=50,
答:m的值为50.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】在半径为25cm的⊙O中,弦AB=40cm,则弦AB所对的弧的中点到AB的距离是( )
A.10cmB.15cmC.40cmD.10cm或40cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E为BC中点连接AE,DF⊥AE于点F,连接CF,FG⊥CF交AD于点G,下列结论:①CF=CD;②G为AD中点;③△DCF∽△AGF;④![]() ,其中结论正确的个数有( )
,其中结论正确的个数有( )
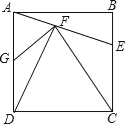
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高1元其销售量就减少20件.
![]() 问应将每件售价定为多少元时,才能使每天利润为640元?
问应将每件售价定为多少元时,才能使每天利润为640元?
![]() 当售价定为多少时,获得最大利润;最大利润是多少?
当售价定为多少时,获得最大利润;最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
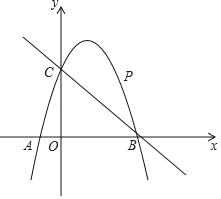
【题目】如图,已知二次函数y=ax2+2x+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0).点P是直线BC上方的抛物线上一动点.
(1)求二次函数y=ax2+2x+c的表达式;
(2)连接PO,PC,并把△POC沿y轴翻折,得到四边形POP′C.若四边形POP′C为菱形,请求出此时点P的坐标;
(3)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.
(1)若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B= °;
(2)如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.
(3)如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
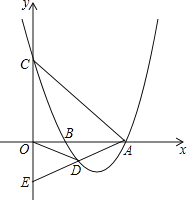
【题目】如图,抛物线y=mx2-16mx+48m(m>0)与x轴交于A、B两点(点B在点A左侧),与y轴交于点C,点D是抛物线上的一个动点,且位于第四象限,连接OD、BD、AC、AD,延长AD交y轴于点E.
(1)若△OAC为等腰直角三角形,求m的值.
(2)若对任意m>0,C、E两点总关于原点对称,求点D的坐标(用含m的式子表示).
(3)当点D运动到某一位置时,恰好使得∠ODB=∠OAD,且点D为线段AE的中点,此时对于该抛物线上任意一点P(x0,y0)总有n≥-4![]() my02-12
my02-12![]() y0-50成立,求实数n的最小值.
y0-50成立,求实数n的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com