
����Ŀ����ͼ��ֱ��![]() ��x�ύ�ڵ�C����y�ύ�ڵ�B��������
��x�ύ�ڵ�C����y�ύ�ڵ�B��������![]() ����B��C���㣮
����B��C���㣮
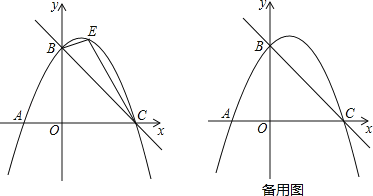
��1���������ߵĽ���ʽ��
��2����ͼ����E���������ϵ�һ���㣨����B��C�����غϣ�����BEC�����ΪS��Sȡ��ֵʱ����Ӧ�ĵ�E����ֻ��������
��3��ֱ��x=2��ֱ��BC�ڵ�M����Q�������߶Գ����ϵĶ��㣬�����������Ƿ���ڵ�P��ʹ����P��Q��A��MΪ������ı�����ƽ���ı��Σ�������ڣ���ֱ��д����P�����ꣻ��������ڣ���˵�����ɣ�
���𰸡���1��y����![]() x2+
x2+![]() x+3����2����S>3ʱ��Ӧ��E������ֻ��2��.��3�����ڣ���P�������ǣ���3����
x+3����2����S>3ʱ��Ӧ��E������ֻ��2��.��3�����ڣ���P�������ǣ���3����![]() ������5����
������5����![]() ��������1��
��������1��![]() ����
����
��������
��1���������B��C�����꣬Ȼ�����ô���ϵ����������������κ����Ľ���ʽ��
��2������E��y���ƽ����EF��ֱ��BC�ڵ�M��EF��x���ڵ�F������E��BC�Ϸ��˶�ʱ�������BEC����������ֵ����ʱ����3���㣻���������3ʱ����Eֻ����BC���·��˶�����Ӧ�ĵ�E����ֻ�����������ɽ��
��3���������⣬�������A�͵�M�����꣬�Լ���Q�ĺ����꣬Ȼ�����ƽ���ı��ε��ж������ʽ��н�𣻿ɷ�Ϊ��������������ۣ��ٵ�AMΪ�Խ���ʱ���ڵ�AQ�ǶԽ���ʱ���۵�MQ�ǶԽ���ʱ�����ɽ������.
�⣺��1����ֱ��y����![]() x+3��x�ύ�ڵ�C����y�ύ�ڵ�B��
x+3��x�ύ�ڵ�C����y�ύ�ڵ�B��
���B�������ǣ�0��3������C�������ǣ�4��0����
��������y��ax2+![]() x+c����B��C���㣬
x+c����B��C���㣬
��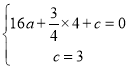 ��
��
��ã�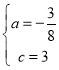 ��
��
��![]() ��
��
��2����ͼ1������E��ֱ��BC�Ϸ��������ϵ�һ����ʱ������E��y���ƽ����EF��ֱ��BC�ڵ�M��EF��x���ڵ�F.
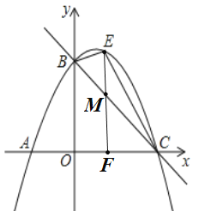
����E��ֱ��BC�Ϸ��������ϵ�һ����ʱ��
���E�������ǣ�x��![]() ����
����
���M�������ǣ�x��![]() ����
����
��EM��![]() ����
����![]() ����
����![]() ��
��
��S��BEC��S��BEM+S��MEC
![]()
��![]()
��![]()
��![]()
��![]() ��
��
��![]() ��
��
�൱x��2ʱ������E�������ǣ�2��3��ʱ����BEC����������������3��
�൱S>3ʱ��Ӧ��E������ֻ��2����
��3���������⣬�����ߵĽ���ʽΪ��![]() ��
��
�������ߵĶԳ���Ϊ��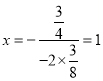 ��
��
���Q�ĺ�����Ϊ1��
��![]() ʱ������ֱ�߷��̣��ã�
ʱ������ֱ�߷��̣��ã�![]() ��
��
���M��������![]() ��
��![]() ����
����
��![]() ����ã�
����ã�![]() ��
��![]() ��
��
���AΪ![]() ����CΪ��4��0����
����C��4��0����
������P��Q��A��MΪ������ı�����ƽ���ı��Σ������������
�ٵ�AMΪ�Խ���ʱ����ͼ��
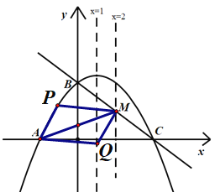
��ʱAM�е�ĺ�����Ϊ����![]() ��
��![]() ����
����
�ߵ�Q�ĺ�����Ϊ1�����P�ĺ�����Ϊ![]() ��
��
��![]() ���������ߵã�
���������ߵã�![]() ��
��
���P��������![]() ��
��![]() ����
����
�ڵ�AQ�ǶԽ���ʱ����ͼ��
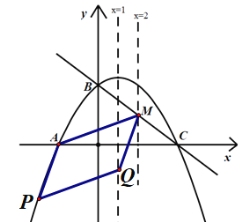
��ʱAQ�е�ĺ�����Ϊ��![]() ��
��
�ߵ�M�ĺ�����Ϊ2�����P�ĺ�����Ϊ![]() ��
��
��![]() ���������ߵã�
���������ߵã�![]() ��
��
���P����![]() ��
��![]() ����
����
�۵�MQ�ǶԽ���ʱ����ͼ��
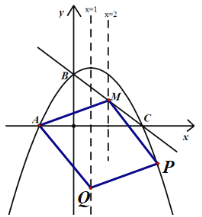
��ʱMQ�е�ĺ�����Ϊ��![]() ��
��
�ߵ�A�ĺ�����Ϊ![]() �����P�ĺ�����Ϊ5��
�����P�ĺ�����Ϊ5��
��![]() ���������߽���ʽ�ã�
���������߽���ʽ�ã�![]() ��
��
���P����![]() ��
��![]() ����
����
�ۺ���������P�������ǣ�����1��![]() ����3��
����3��![]() ����5��
����5��![]() ����
����


 �����Ծ���ĩ���100��ϵ�д�
�����Ծ���ĩ���100��ϵ�д� ˫��ͬ������ѵ��ϵ�д�
˫��ͬ������ѵ��ϵ�д� �Ƹ�С״Ԫͬ������������ϵ�д�
�Ƹ�С״Ԫͬ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Сˮ������һյ·�ƣ���֪֧��AB�ij���0.8m��A�˵�����ľ���AC��4m��֧��AB�����AC�ļн�Ϊ65����С����ˮ�ص�����D���֧��B�˵�������45������ˮ�ص�����E���֧��A�˵�������50������C��E��D��ͬһֱ���ϣ�����Сˮ�صĿ�DE���������ȷ��0.1m����sin65���0.9��cos65���0.4��tan50���1.2��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
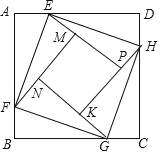
����Ŀ����ͼ������ABCD�ı߳�Ϊ2����E��F��G��H�ֱ���AD��AB��BC��CD�ϣ���EA=FB=GC=HD���ֱ���AEF����BFG����CGH����DHE��EF��FG��GH��HE���ۣ����ı���MNKP����AE=x��0��x��1����S�ı���MNKP=y����y����x�ĺ���ͼ�����Ϊ��������
A. 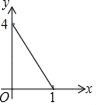 B.
B. 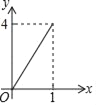 C.
C.  D.
D. 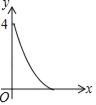
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ijƷ����Ʒ�����ۣ���֪��Ʒ����Ʒ����ÿ��40Ԫ��������y�����������ۼ�x��Ԫ/����֮��Ĺ�ϵ��ͼ��ʾ��ʵ�ߣ�����Ա���Ĺ���ÿ��ÿ��100Ԫ��ÿ�컹Ӧ֧����������150Ԫ��

��1����������y�����������ۼ�x��Ԫ/����֮��ĺ�����ϵʽ��
��2���õ�Ա���˹�3�ˣ���ij����֧ǡ��ƽ�⣨���룽֧��������������ۼ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���![]() ��ͼ���������ύ�ڵ�A��1�� 0���͵�C��������A��ֱ��
��ͼ���������ύ�ڵ�A��1�� 0���͵�C��������A��ֱ��![]() ����κ���ͼ������һ��B����B���C���ڶ��κ���ͼ��ĶԳ���Գƣ�
����κ���ͼ������һ��B����B���C���ڶ��κ���ͼ��ĶԳ���Գƣ�
��1����һ�κ�������ʽ��
��2����P�ڶ��κ���ͼ��ĶԳ����ϣ�����ACP���ܳ���Сʱ���������P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪Rt��ABC�У���C��90����AC��6��BC��8����P��ÿ��1����λ���ٶȴ�A��C�˶���ͬʱ��Q��ÿ��2����λ���ٶȴ�B��A�����˶���Q����A���P��Ҳֹͣ�˶������P��Q�˶���ʱ��Ϊt�룮
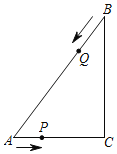
��1����P��ֹͣ�˶�ʱ��BP�ij���
��2��P��Q�������˶������У���E��Q�����ֱ��AC�ĶԳƵ㣬�Ƿ����ʱ��t��ʹ�ı���PQCEΪ���Σ������ڣ������ʱt��ֵ���������ڣ���˵�����ɣ�
��3��P��Q�������˶������У���ʹ��APQ����ABC���Ƶ�ʱ��t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�������һ�����ĸ߶ȣ�����������Ӱ��ǡ�����ڵ����һб���ϣ���ͼ����ʱ��õ����ϵ�Ӱ��Ϊ8���������ϵ�Ӱ��Ϊ4������֪б�µ��½�Ϊ300��ͬһʱ �̣�һ����Ϊl�ס���ֱ�ڵ�������ı���ڵ����ϵ�Ӱ��Ϊ2���������ĸ߶�Ϊ�� ��
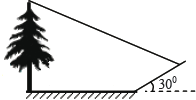
A.![]() �� B.12�� C.
�� B.12�� C.![]() �� D��10��
�� D��10��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
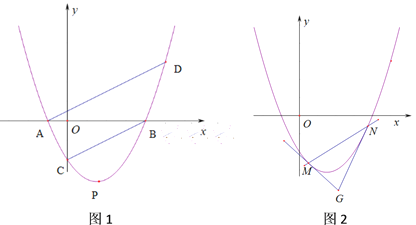
����Ŀ����֪������![]() ��
��![]() �ύ��A��B����(A��B���)����
�ύ��A��B����(A��B���)����![]() �ύ��C�㣬����ΪP��OC=2AO.
�ύ��C�㣬����ΪP��OC=2AO.
(1)��![]() ��
��![]() ����Ĺ�ϵʽ��
����Ĺ�ϵʽ��
(2)ֱ��AD//BC���������߽�����һ��D����ADP�����Ϊ![]() ����
����![]() ��ֵ��
��ֵ��
(3)��(2)�������£���(1��-1)��ֱ���������߽���M��N���㣬�ֱ��M��N���������߽���һ�������������ֱ�߽��ڵ�G����OG������Сֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com