
【题目】已知如图所示,在Rt△ABC中,∠A=90°,∠BCA=75°,AC=8cm,DE垂直平分BC,则BE的长是( )
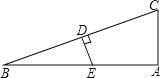
A.4cmB.8cmC.16cmD.32cm
科目:初中数学 来源: 题型:
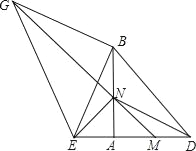
【题目】如图,等腰Rt△ABD中,AB=AD,点M 为边AD上一动点,点E在DA的延长线上,且AM=AE,以BE为直角边,向外作等腰Rt△BEG,MG交AB于N,连NE、DN.
(1)求证:∠BEN=∠BGN.
(2)求![]() 的值.
的值.
(3)当M在AD上运动时,探究四边形BDNG的形状,并证明之.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )

A. DE=EB B. ![]() DE=EB C.
DE=EB C. ![]() DE=DO D. DE=OB
DE=DO D. DE=OB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了m人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.

(1)根据图中信息求出m= ,n= ;
(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生中,大约有多少人最认可“微信”这一新生事物?
(4)已知A、B两位同学都最认可“微信”,C同学最认可“支付宝”D同学最认可“网购”从这四名同学中抽取两名同学,请你通过树状图或表格,求出这两位同学最认可的新生事物不一样的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂设计了一款成本为20元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价 | … | 30 | 40 | 50 | 60 | … |
每天销售量 | … | 500 | 400 | 300 | 200 | … |
(1)研究发现,每天销售量![]() 与单价
与单价![]() 满足一次函数关系,求出
满足一次函数关系,求出![]() 与
与![]() 的关系式;
的关系式;
(2)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润8000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )

A. 21.7米 B. 22.4米 C. 27.4米 D. 28.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育老师统计了七年级甲、乙两个班女生的身高,并绘制了以下不完整的统计图.

请根据图中信息,解决下列问题:
(1)两个班共有女生多少人?
(2)将频数分布直方图补充完整;
(3)求扇形统计图中![]() 部分所对应的扇形圆心角度数;
部分所对应的扇形圆心角度数;
(4)身高在![]() 的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率.
的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若x1、x2是关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:![]() ,
,![]() .我们把它们称为根与系数关系定理.
.我们把它们称为根与系数关系定理.
如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:AB=![]() =
=![]() =
=![]() =
=![]() =
=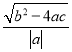
请你参考以上定理和结论,解答下列问题:
设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.
(1)当△ABC为等腰直角三角形时,直接写出b2-4ac的值;
(2)当△ABC为等腰三角形,且∠ACB=120°时,直接写出b2-4ac的值;
(3)设抛物线y=x2+mx+5与x轴的两个交点为A、B,顶点为C,且∠ACB=90°,试问如何平移此抛物线,才能使∠ACB=120°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,等边△AEF的顶点E、F分别在BC和CD上.
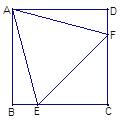
(1)、求证:△ABE≌△ADF;
(2)、若等边△AEF的周长为6,求正方形ABCD的边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com