
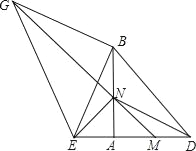
【题目】如图,等腰Rt△ABD中,AB=AD,点M 为边AD上一动点,点E在DA的延长线上,且AM=AE,以BE为直角边,向外作等腰Rt△BEG,MG交AB于N,连NE、DN.
(1)求证:∠BEN=∠BGN.
(2)求![]() 的值.
的值.
(3)当M在AD上运动时,探究四边形BDNG的形状,并证明之.
【答案】(1)详见解析;(2)![]() ;(3)四边形BDNG是平行四边形,证明详见解析.
;(3)四边形BDNG是平行四边形,证明详见解析.
【解析】
(1)连接BM,推出BE=BM,∠EBA=∠MBA,根据SAS证△BMN≌△BEN,推出∠BMN=∠BEN,证出∠BMN=∠BGN即可;
(2)过G作GH⊥AB,垂足为H,证△BGH≌△ABE,推出BH=AE=AN,求出NG=![]() GH=
GH=![]() AB,代入求出即可;
AB,代入求出即可;
(3)根据ADN≌△BAE,推出BG⊥BE,BG=BE,得出BG∥DN,BG=DN,根据平行四边形的判定判断即可.
(1)证明:连BM,
∵∠BAD=90°,
∴BA⊥EM,
∵AE=AM,
∴BE=BM,∠EBA=∠MBA,
在△BEN和△BMN中
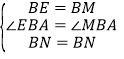 ,
,
∴△BMN≌△BEN,
∴∠BMN=∠BEN,
∵BE=BG=BM,
∴∠BMN=∠BGN,
∴∠BEN=∠BGN.
(2)解:由(1)得,∠GBE=∠GNE=90°,
∴△NME等腰直角三角形,
∴AE=AN,
过G作GH⊥AB,垂足为H,
∴∠H=∠BAE=∠GBE=90°,
∴∠HGB+∠HBG=90°,∠HBG+∠ABE=90°,
∴∠HGB=∠EBA,
在△BGH和△ABE中
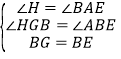 ,
,
∴△BGH≌△ABE,
∴BH=AE=AN,
HN=AB=GH,NG=![]() GH=
GH=![]() AB,
AB,
∴![]() .
.
(3)解:四边形BDNG是平行四边形,
理由是:∵∠DAN=∠BAE=90°,AN=AE,AB=AD,
∴△ADN≌△BAE,
∴DN⊥BE,DN=BE=BG,
又∵BG⊥BE,BG=BE,
∴BG∥DN,BG=DN
∴四边形BDNG为平行四边形.


科目:初中数学 来源: 题型:
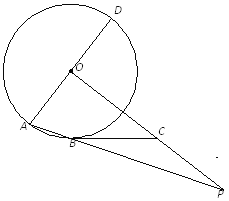
【题目】如图,AD是⊙O的直径,AB为⊙O 的弦,OP⊥AD,OP与AB的延长线交于点P.点C在OP上,且BC=PC.
(1)求证:直线BC是⊙O的切线;
(2)若OA=3,AB=2,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药厂两年前生产1t某种药品的成本是5000元,随着生产技术的进步,现在生产1t该种药品的成本是3000元.设该种药品生产成本的年平均下降率为x,则下列所列方程正确的是( )
A. 5000×2(1﹣x)=3000 B. 5000×(1﹣x)2=3000
C. 5000×(1﹣2x)=3000 D. 5000×(1﹣x2)=3000
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某广场上有一个形状是平行四边形的花坛(如图),分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果有AB∥EF∥DC,BC∥GH∥AD,那么下列说法错误的是( )
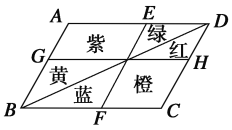
A. 红花、绿花种植面积一定相等
B. 紫花、橙花种植面积一定相等
C. 红花、蓝花种植面积一定相等
D. 蓝花、黄花种植面积一定相等
查看答案和解析>>
科目:初中数学 来源: 题型:
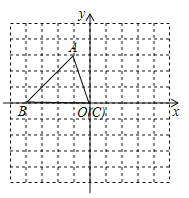
【题目】(2016黑龙江省齐齐哈尔市)如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣4,0),C(0,0)
(1)画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;
(2)画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O;
(3)在x轴上存在一点P,满足点P到A1与点A2距离之和最小,请直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合).在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AF=![]() AE;
AE;
(3)如图3,将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=2![]() ,CE=2,求线段AE的长.
,CE=2,求线段AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=3,BC=2![]() ,点E在BC边上,连接DE,将△DEC沿DE翻折,得到△DEC',C'E交AD于点F,连接AC'.若点F为AD的中点,则AC′的长度为( )
,点E在BC边上,连接DE,将△DEC沿DE翻折,得到△DEC',C'E交AD于点F,连接AC'.若点F为AD的中点,则AC′的长度为( )
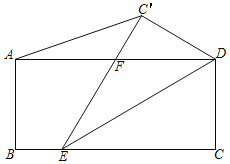
A.![]() B.2
B.2![]() C.2
C.2![]() D.
D.![]() +1
+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com