
【题目】小明在学完了平行四边形这个章节后,想对“四边形的不稳定性”和“四边形的判定”有更好的理解,做了如下的探究:他将8个木棍和一些钉子组成了一个正方形![]() 和平行四边形
和平行四边形![]() (如图1),且
(如图1),且![]() ,
,![]() 在一条直线上,点
在一条直线上,点![]() 落在边
落在边![]() 上.经小明测量,发现此时
上.经小明测量,发现此时![]() 、
、![]() 、
、![]() 三个点在一条直线上,
三个点在一条直线上,![]() ,
,![]() .
.

(1)求![]() 的长度;
的长度;
(2)设![]() 的长度为
的长度为![]() ,
,![]() ________(用含
________(用含![]() 的代数式表示);
的代数式表示);
(3)小明接着探究,在保证![]() ,
,![]() 位置不变的前提条件下,从点
位置不变的前提条件下,从点![]() 向右推动正方形,直到四边形
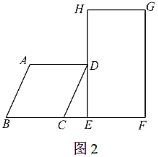
向右推动正方形,直到四边形![]() 刚好变为矩形时停止推动(如图2).若此时
刚好变为矩形时停止推动(如图2).若此时![]() ,求
,求![]() 的长度.
的长度.
科目:初中数学 来源: 题型:
【题目】小明外出游玩时,带了![]() 件上衣和
件上衣和![]() 条长裤,上衣颜色有白色、蓝色,长裤有白色、黑色、蓝色,随意拿出一条裤子和一件上衣问题为:
条长裤,上衣颜色有白色、蓝色,长裤有白色、黑色、蓝色,随意拿出一条裤子和一件上衣问题为:
(![]() )小明随意拿出一条裤子和一件上衣配成一套,列出所有可能出现结果的“树状图”;
)小明随意拿出一条裤子和一件上衣配成一套,列出所有可能出现结果的“树状图”;
(![]() )他任意拿出一件上衣和一条长裤穿上的颜色正好相同的概率是多少?
)他任意拿出一件上衣和一条长裤穿上的颜色正好相同的概率是多少?
(![]() )小明正好拿出黑色长裤的概率是多少?
)小明正好拿出黑色长裤的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
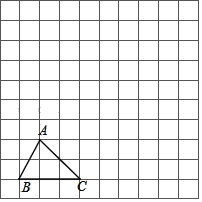
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(顶点是网格线的交点).
(1)先将△ABC竖直向上平移6个单位,再水平向右平移3个单位得到△A1B1C1,请画出△A1B1C1;
(2)将△A1B1C1绕B1点顺时针旋转90°,得△A2B2C2,请画出△A2B2C2;
(3)连接CA2,直接写出CA2的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
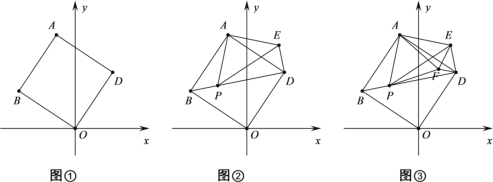
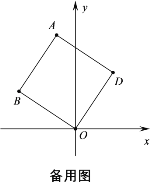
【题目】如图①,将正方形ABOD放在平面直角坐标系中,O是坐标原点,点D的坐标为(2,3),
(1)点B的坐标为 ;
(2)若点P为对角线BD上的动点,作等腰直角三角形APE,使∠PAE=90°,如图②,连接DE,则BP与DE的关系(位置与数量关系)是 ,并说明理由;
(3)在(2)的条件下,再作等边三角形APF,连接EF、FD,如图③,在 P点运动过程中当EF取最小值时,此时∠DFE= °;
(4)在(1)的条件下,点 M在 x 轴上,在平面内是否存在点N,使以 B、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
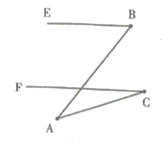
【题目】如图(a),木杆EB与FC平行,木杆的两端B,C用一橡皮筋连接,现将图(a)中的橡皮筋拉成下列各图的形状,试解答下列各题:

(1)探究图(b)、(c)、(d)、(e)中,![]() 之间的数量关系,并填空;
之间的数量关系,并填空;
①图(b)中,![]() 之间的关系是________________________;
之间的关系是________________________;
②图(c)中,![]() 之间的关系是_________________________;
之间的关系是_________________________;
③图(d)中,![]() 之间的关系是__________________________;
之间的关系是__________________________;
④图(e)中,![]() 之间的关系是__________________________;
之间的关系是__________________________;
(2)探究图(f)、(g)中,![]() 之间的数量关系,并填空:
之间的数量关系,并填空:
①图(f)中,![]() 之间的关系是________________________________;
之间的关系是________________________________;
②图(g)中,![]() 之间的关系是________________________________;
之间的关系是________________________________;
(3)请对图(e)的结论加以证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形![]() 的对角线交于点
的对角线交于点![]() ,
,![]() .
.
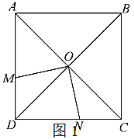
(1)如图1,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,求证:
上,求证:![]() ;
;
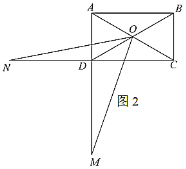
(2)如图2,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 的延长线上,点
的延长线上,点![]() 在线段
在线段![]() 的延长线上,若
的延长线上,若![]() ,求
,求![]() 的值;
的值;
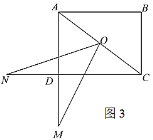
(3)如图3,![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 的延长线上,点
的延长线上,点![]() 在线段
在线段![]() 的延长线上,若
的延长线上,若![]() ,直接写出线段
,直接写出线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠BAD, ∠ACD=∠ABC=90°,E、F分别为AC、CD的中点,∠D=62°,则∠BEF的度数为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青年志愿者爱心小分队赴山村送温暖,准备为困难村民购买一些米面.已知购买1袋大米、4袋面粉,共需240元;购买2袋大米、1袋面粉,共需165元.
(1)求每袋大米和面粉各多少元?
(2)如果爱心小分队计划购买这些米面共40袋,总费用不超过2140元,那么至少购买多少袋面粉?
查看答案和解析>>
科目:初中数学 来源: 题型:
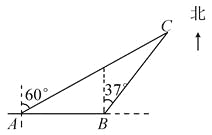
【题目】一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发生了求救信号,一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里/时的速度前往救援,求海警船到达事故船C处所需的大约时间.(参考数据:sin53°≈0.8,cos53°≈0.6)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com