
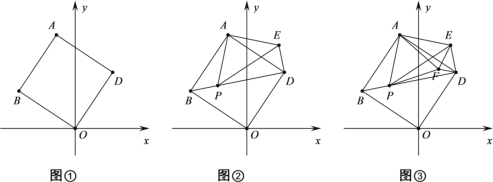
【题目】如图①,将正方形ABOD放在平面直角坐标系中,O是坐标原点,点D的坐标为(2,3),
(1)点B的坐标为 ;
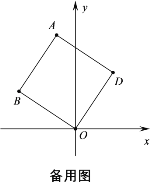
(2)若点P为对角线BD上的动点,作等腰直角三角形APE,使∠PAE=90°,如图②,连接DE,则BP与DE的关系(位置与数量关系)是 ,并说明理由;
(3)在(2)的条件下,再作等边三角形APF,连接EF、FD,如图③,在 P点运动过程中当EF取最小值时,此时∠DFE= °;
(4)在(1)的条件下,点 M在 x 轴上,在平面内是否存在点N,使以 B、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.
【答案】(1)点B的坐标为(-3,2);(2)BP与DE的关系是垂直且相等,证明详见解析;(3)∠DFE= 150 °;(4)存在,点N坐标为(![]() +2,1)或(-
+2,1)或(-![]() +2,1)或(
+2,1)或(![]() -3,-1)或(-
-3,-1)或(-![]() -3,-1)或(-1,5)
-3,-1)或(-1,5)
【解析】
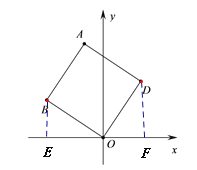
(1)如图,过点B作BE⊥x轴于E,过点D作DF⊥x轴于F,证明△BEO≌△OFD,则可得OF=BE,OE=FD,根据点D的坐标(2,3),可求得点B坐标;
(2)如图,通过证明△ABP≌△ADE(SAS),可得∠4=∠5,BP=DE,进而可证明∠BDE=90°,则,BP与DE垂直且相等得证;
(3)由等边△APF和等腰直角△PAE,可知△AFE为等腰三角形,顶角为30°,且EF为底边,所以当腰AF最小时,底边EF则最小,故而AP垂直BD时,AF=AP此时取最小值,此时易证△AFE≌△PFD,故而∠AFE=∠PFD=75°,根据周角为360°,即可计算∠EFD的度数;
(4)分情况讨论,①当BD为菱形的边时,通过作图构造直角三角形,使用勾股定理先求对应点M坐标,再根据菱形的性质及平移思想,求点N坐标;②当BD为菱形的对角线时,M与O重合,此时N与A重合,同样构造直角三角形,使用勾股定理求解即可.
解(1):过点B作BE⊥x轴于E,过点D作DF⊥x轴于F,
∵ABOD为正方形,O是坐标原点,点D的坐标为(2,3),
∴OB=OD,∠BE0=∠DFO,∠BOE=∠ODF,
∴△BEO≌△OFD,
∴OF=BE,OE=FD,
∴点B的坐标为(-3,2),
故答案为:(-3,2);
(2)BP与DE的关系是:垂直且相等;
证明:如图,
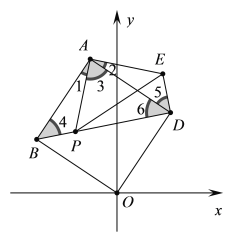
∵正方形ABOD,
∴∠BAD=90°,AB=AD,
∵∠PAE=90°,
∴∠BAD-∠3=∠PAE-∠3,
即∠1=∠2,
∵AP=AE,
∴△ABP≌△ADE(SAS),
∴∠4=∠5, BP=DE,
∵∠4+∠6=90°,
∴∠5+∠6=90°,
即∠BDE=90°,
∴BP⊥DE,
∴BP与DE垂直且相等,
故答案为:垂直且相等;
(3)∵△APF为等边三角形,△PAE为等腰直角三角形,且∠PAE=90°,
∴AF=AE,∠FAE=30°,
即△AFE为等腰三角形,且EF为底边,
∴当EF最小时,AF=AE应该取最小值,即AP应当取最小值,
∵四边形ABOD为矩形,BD为ABOD一条对角线,
∴当AP⊥BD时,EF有最小值,如下图所示,
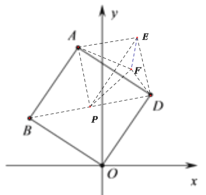
∴AP=PD=AE,∠PAD=∠APD=90°,
∴∠EAF=∠DPF=30°,
又∵AF=PF,
∴△AFE≌△PFE,
∴∠PFD=∠AFE=75°,
∴∠EFD=360°-75°-75°-60°=150°,
即,当EF取最小值时,∠DFE=150°,
故答案为:150;
(4)∵D(2,3),
∴OD=![]() ,
,
∴BD=![]() ,
,
①当BD为菱形的边时,
(Ⅰ)如图,作BQ⊥x轴于Q,
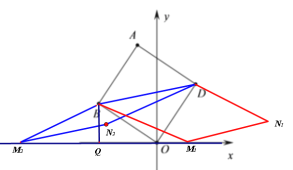
MB=BD=![]() ,在Rt△BQM中根据勾股定理,可得M1(
,在Rt△BQM中根据勾股定理,可得M1(![]() -3,0)、M2(-
-3,0)、M2(-![]() -3,0),
-3,0),
∵B向右平移5个单位再向上平移1个单位得到D,
∴N1(![]() +2,1)、N2(-
+2,1)、N2(-![]() +2,1);
+2,1);
(Ⅱ)如图,作TP垂直x轴于P,
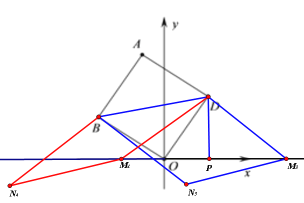
MD=BD=![]() ,在Rt△DPM中根据勾股定理,可得M3(
,在Rt△DPM中根据勾股定理,可得M3(![]() +2,0)、M4(-
+2,0)、M4(-![]() +2,0),
+2,0),
∵D向左平移5个单位再向下平移1个单位得到B,
∴N3(![]() -3,-1)、N4(-
-3,-1)、N4(-![]() -3,-1)
-3,-1)
②当BD为菱形的对角线时,M与O重合,此时N与A重合,
如图,作AJ∥x轴交y轴于R,过点D作JK⊥x轴垂足为K,交AJ于点J,
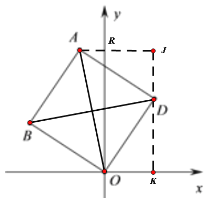
易证△ALD≌△DKO,
∴JK=5,
在Rt△ARO中使用勾股定理,即可求N5(-1,5),
综上所述,点N坐标为(![]() +2,1)或(-
+2,1)或(-![]() +2,1)或(
+2,1)或(![]() -3,-1)或(-
-3,-1)或(-![]() -3,-1)或(-1,5).
-3,-1)或(-1,5).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.
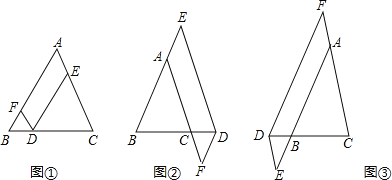
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).

(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)有甲、乙两个不透明的盒子,甲盒子中装有3张卡片,卡片上分别写着3![]() 、7
、7![]() 、9
、9![]() ;乙盒子中装有4张卡片,卡片上分别写着2
;乙盒子中装有4张卡片,卡片上分别写着2![]() 、4
、4![]() 、6
、6![]() 、8
、8![]() ;盒子外有一张写着5
;盒子外有一张写着5![]() 的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
(1)请用树状图或列表的方法求这三条线段能组成三角形的概率;
(2)求这三条线段能组成直角三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由49个边长为1的小正方形组成的7×7的正方形网格,小正方形的顶点为格点,点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 均在格点上.
均在格点上.

(1)直接写出![]() ________;
________;
(2)点![]() 在网格中的格点上,且
在网格中的格点上,且![]() 是以
是以![]() 为顶角顶点的等腰三角形,则满足条件的点
为顶角顶点的等腰三角形,则满足条件的点![]() 有________个;
有________个;
(3)请在如图所示的网格中,借助矩形![]() 和无刻度的直尺作出
和无刻度的直尺作出![]() 的角平分线,并保留作图痕迹.
的角平分线,并保留作图痕迹.
查看答案和解析>>
科目:初中数学 来源: 题型:
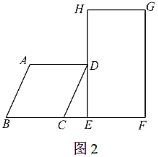
【题目】小明在学完了平行四边形这个章节后,想对“四边形的不稳定性”和“四边形的判定”有更好的理解,做了如下的探究:他将8个木棍和一些钉子组成了一个正方形![]() 和平行四边形
和平行四边形![]() (如图1),且
(如图1),且![]() ,
,![]() 在一条直线上,点
在一条直线上,点![]() 落在边
落在边![]() 上.经小明测量,发现此时
上.经小明测量,发现此时![]() 、
、![]() 、
、![]() 三个点在一条直线上,
三个点在一条直线上,![]() ,
,![]() .
.

(1)求![]() 的长度;
的长度;
(2)设![]() 的长度为
的长度为![]() ,
,![]() ________(用含
________(用含![]() 的代数式表示);
的代数式表示);
(3)小明接着探究,在保证![]() ,
,![]() 位置不变的前提条件下,从点
位置不变的前提条件下,从点![]() 向右推动正方形,直到四边形
向右推动正方形,直到四边形![]() 刚好变为矩形时停止推动(如图2).若此时
刚好变为矩形时停止推动(如图2).若此时![]() ,求
,求![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
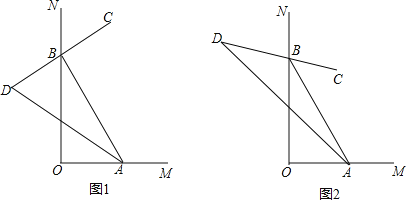
【题目】如图,∠MON=90°,点A、B分别在OM、ON上运动(不与点O重合).
(1)如图①,BC是∠ABN的平分线,BC的反方向延长线与∠BAO的平分线交于点D.
①若∠BAO=60°,则∠D的大小为 度,
②猜想:∠D的度数是否随A、B的移动发生变化?请说明理由.
(2)如图②,若∠ABC=![]() ∠ABN, ∠BAD=
∠ABN, ∠BAD=![]() ∠BAO,则∠D的大小为 度,若∠ABC=
∠BAO,则∠D的大小为 度,若∠ABC=![]() ∠ABN, ∠BAD=
∠ABN, ∠BAD=![]() ∠BAO,则∠D的大小为 度(用含n的代数式表示).
∠BAO,则∠D的大小为 度(用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
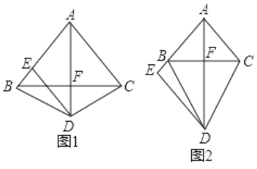
【题目】如图1,已知△ABC中,AB=AC,点D是△ABC外一点(与点A分别在直线BC两侧).且DB=DC,过点D作DE//AC,交射线AB于E,连接AD交BC于F.
(1)求证:AD垂直BC;
(2)如图1,点E在线段AB上且不与B重合时,求证:DE=AE;
(3)如图2,当点E在线段AB的延长线上时,请直接写出线段DE,AC,BE的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com