
【题目】在平面直角坐标系xOy中,⊙C的半径为r(r>1),P是圆内与圆心C不重合的点,⊙C的“完美点”的定义如下:若直线CP与⊙C交于点A,B,满足|PA﹣PB|=2,则称点P为⊙C的“完美点”,如图为⊙C及其“完美点”P的示意图.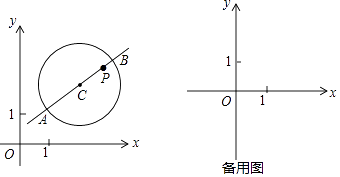
(1)当⊙O的半径为2时,
①点M( ![]() ,0)⊙O的“完美点”,点N(0,1)⊙O的“完美点”,点T(﹣
,0)⊙O的“完美点”,点N(0,1)⊙O的“完美点”,点T(﹣ ![]() ,﹣
,﹣ ![]() )⊙O的“完美点”(填“是”或者“不是”);
)⊙O的“完美点”(填“是”或者“不是”);
②若⊙O的“完美点”P在直线y= ![]() x上,求PO的长及点P的坐标;
x上,求PO的长及点P的坐标;
(2)⊙C的圆心在直线y= ![]() x+1上,半径为2,若y轴上存在⊙C的“完美点”,求圆心C的纵坐标t的取值范围.
x+1上,半径为2,若y轴上存在⊙C的“完美点”,求圆心C的纵坐标t的取值范围.
【答案】
(1)不是;是;是;解:根据题意,,PA﹣PB,=2,∴,OP+2﹣(2﹣OP),=2,∴OP=1.若点P在第一象限内,作PQ⊥x轴于点Q,如图1中,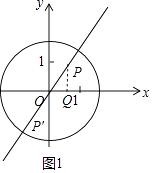 ∵点P在直线y=
∵点P在直线y= ![]() x上,OP=1,∴OQ=
x上,OP=1,∴OQ= ![]() ,PQ=
,PQ= ![]() .∴P(
.∴P( ![]() ,
,![]() ).若点P在第三象限内,根据对称性可知其坐标为(﹣
).若点P在第三象限内,根据对称性可知其坐标为(﹣ ![]() ,﹣
,﹣ ![]() ).综上所述,PO的长为1,点P的坐标为(
).综上所述,PO的长为1,点P的坐标为( ![]() ,
,![]() )或(﹣
)或(﹣ ![]() ,﹣
,﹣ ![]() )
)
(2)解:对于⊙C的任意一个“完美点”P都有|PA﹣PB|=2,
∴|CP+2﹣(2﹣CP)|=2.
∴CP=1.
∴对于任意的点P,满足CP=1,都有|CP+2﹣(2﹣CP)|=2,
∴|PA﹣PB|=2,故此时点P为⊙C的“完美点”.因此,⊙C的“完美点”是以点C为圆心,1为半径的圆.
如图2中,设直线y= ![]() x+1与y轴交于点D,当⊙C移动到与y轴相切且切点在点D的下方时,t的值最小.
x+1与y轴交于点D,当⊙C移动到与y轴相切且切点在点D的下方时,t的值最小.
设切点为E,连接CE,
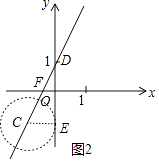
∵⊙C的圆心在直线y= ![]() x+1上,
x+1上,
∴此直线和x轴,y轴的交点C(0,1),F(﹣ ![]() ,0),
,0),
∴OF= ![]() ,OD=1,
,OD=1,
∵CE∥OF,
∴△DOF∽△DEC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴DE= ![]() ,t的最小值为1﹣
,t的最小值为1﹣ ![]() .
.
当⊙C移动到与y轴相切且切点在点D的上方时,t的值最大.
同理可得t的最大值为1+ ![]() .
.
综上所述,t的取值范围为1﹣ ![]() ≤t≤1+
≤t≤1+ ![]()
【解析】解:(1)点M不是⊙O的“完美点”,
点N是⊙O的“完美点”,
点T是⊙O的“完美点”.
所以答案是不是,是,是.


科目:初中数学 来源: 题型:
【题目】已知:A(0,1),B(2,0),C(4,3)
(1)在直角坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图1,平行四边形ABCD中,点O是对角线AC的中点,EF过点O,与AD,BC分别相交于点E,F,GH过点O,与AB,CD分别相交于点G,H,连接EG,FG,FH,EH.

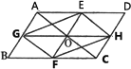
(1)求证:四边形EGFH是平行四边形;
(2)如图2,若EF//AB,GH//BC,在不添加任何辅助线的情况下,请直接写出图2中与四边形AGHD面积相等的所有平行四边形(四边形AGHD除外).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B两点的坐标分别为(﹣2,0)、(0,1),⊙C 的圆心坐标为(0,﹣1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是( ) 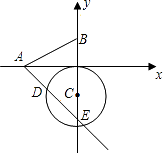
A.3
B.![]()
C.![]()
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金湖中学社团活动开展地丰富多彩.七年级数学社团课上同学们在探究一数值转换器,原理如图所示.开始输入x值为5,可发现第一次输出的结果是8,第2次输出结果是4,依次下去…,第2018次输出的结果是__.
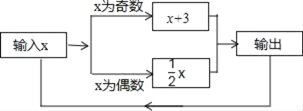
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.

求证:(1)△AFD≌△CEB.(2)四边形ABCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点
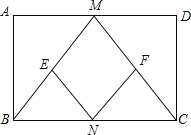
(1)求证:△ABM≌△DCM
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB= _时,四边形MENF是正方形(只写结论,不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在同一条直线上,M,N分别为BE,CD的中点.
(1)求证:△ABE≌ACD;
(2)判断△AMN的形状,并说明理由.
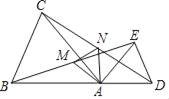
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com