

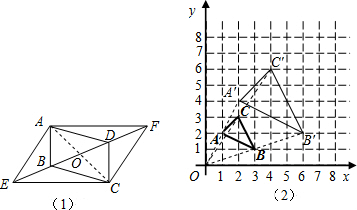
 (1)证明:如图(1),连接AC交EF于O,
(1)证明:如图(1),连接AC交EF于O,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 我国网球名将李娜在今年法国网球公开赛上的出色表现,大大激发了国人对网球的热情.在一项“你最喜欢的球类运动”的调查中,共有50名同学参与调查,每人必选且只选一项,将调查结果绘制成频数分布直方图如下,根据图中信息回答:
我国网球名将李娜在今年法国网球公开赛上的出色表现,大大激发了国人对网球的热情.在一项“你最喜欢的球类运动”的调查中,共有50名同学参与调查,每人必选且只选一项,将调查结果绘制成频数分布直方图如下,根据图中信息回答:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,正方形网格中的每个小正方形边长都是1.已知A、B是两格点,若△ABC为等腰三角形,且S△ABC=1.5,则满足条件的格点C有( )
如图,正方形网格中的每个小正方形边长都是1.已知A、B是两格点,若△ABC为等腰三角形,且S△ABC=1.5,则满足条件的格点C有( )| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 某校为开展“阳光体育”运动,丰富学生课间自由活动内容,随机选取了本校100名学生进行调查,调查的内容是:你最喜欢的自由活动项目是什么?并将收集到的数据整理,绘出了如图所示的统计图.
某校为开展“阳光体育”运动,丰富学生课间自由活动内容,随机选取了本校100名学生进行调查,调查的内容是:你最喜欢的自由活动项目是什么?并将收集到的数据整理,绘出了如图所示的统计图.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com