
一等腰三角形底边长为8cm,腰长为5cm,则腰上的高为( )
A.3cm B.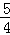 cm C.
cm C.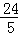 cm D.
cm D.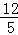 cm
cm
C【考点】勾股定理;等腰三角形的性质.
【分析】作AD⊥BC于D,作CE⊥AB于E,由等腰三角形的性质得出BD,由勾股定理求出AD,由三角形面积的计算方法即可求出腰上的高.
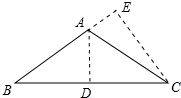
【解答】解:如图所示:
作AD⊥BC于D,作CE⊥AB于E,
则∠ADB=90°,
∵AB=AC,
∴BD=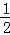 BC=4cm,
BC=4cm,
∴AD=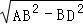 =
=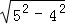 =3(cm),
=3(cm),
∵△ABC的面积=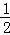 AB•CE=
AB•CE=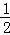 BC•AD,
BC•AD,
∴AB•CE=BC•AD,
即5×CE=8×3,
解得:CE=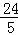 ,
,
即腰上的高为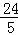 ;
;
故选:C.
【点评】本题考查了勾股定理、等腰三角形的性质三角形面积的计算;熟练掌握等腰三角形的性质,运用勾股定理求出AD是解决问题的关键.


科目:初中数学 来源: 题型:
在下列各组条件中,不能说明△ABC≌△DEF的是( )
A.AB=DE,∠B=∠E,∠C=∠F B.AC=DF,BC=EF,∠A=∠D
C.AB=DE,∠A=∠D,∠B=∠E D.AB=DE,BC=EF,AC=DF
查看答案和解析>>
科目:初中数学 来源: 题型:
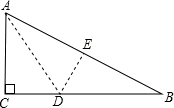
如图,有一块直角三角形纸片,两直角边AC=3cm,BC=4cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,Rt△ABC中,∠B=90°,AB=9,BC=6,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段AN的长等于( )
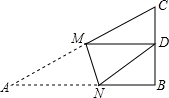
A.3 B.4 C.5 D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com