
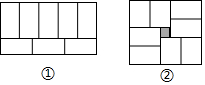
 小亮用8个同样大小的长方形,拼成了一个大的长方形(图①).小莹用这8个长方形拼成了正方形(图②),但是中间空出了一个边长为2的小正方形,你能根据图①和图②求出小长方形的长和宽吗?
小亮用8个同样大小的长方形,拼成了一个大的长方形(图①).小莹用这8个长方形拼成了正方形(图②),但是中间空出了一个边长为2的小正方形,你能根据图①和图②求出小长方形的长和宽吗? 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
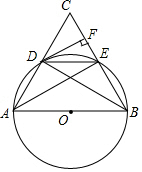 如图,AB为⊙O的直径,点C为圆外一点,连接AC、BC,分别与⊙O相交于点D、点E,且$\widehat{AD}$=$\widehat{DE}$,过点D作DF⊥BC于点F,连接BD、DE、AE.
如图,AB为⊙O的直径,点C为圆外一点,连接AC、BC,分别与⊙O相交于点D、点E,且$\widehat{AD}$=$\widehat{DE}$,过点D作DF⊥BC于点F,连接BD、DE、AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两商场春节期间都进行让利酬宾活动,其中,甲商场对一次购物超过200元部分打7折(不超过200元部分按原价)优惠,如图所示,表示甲商场在让利方式下购物金额y(元)关于商品原价x(元)的函数图象;若乙商场所有商品按8折出售,请在同一坐标系下画出乙商场在让利方式下y关于x的函数图象,并利用图象说明如何选择这两家商场购物更省钱.
甲、乙两商场春节期间都进行让利酬宾活动,其中,甲商场对一次购物超过200元部分打7折(不超过200元部分按原价)优惠,如图所示,表示甲商场在让利方式下购物金额y(元)关于商品原价x(元)的函数图象;若乙商场所有商品按8折出售,请在同一坐标系下画出乙商场在让利方式下y关于x的函数图象,并利用图象说明如何选择这两家商场购物更省钱.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
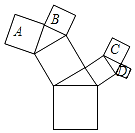 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,正方形A的边长为6cm、B的边长为5cm、C的边长为5cm,则正方形D的边长为( )
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,正方形A的边长为6cm、B的边长为5cm、C的边长为5cm,则正方形D的边长为( )| A. | $\sqrt{14}$cm | B. | 4 cm | C. | $\sqrt{15}$cm | D. | 3 cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是一条河,A、B是对岸两点(AB垂直河岸),某同学站在B点,在不能到达对岸的情况下,请你帮他设计至少两种方案求出A、B之间的距离,并请说明理由.
如图是一条河,A、B是对岸两点(AB垂直河岸),某同学站在B点,在不能到达对岸的情况下,请你帮他设计至少两种方案求出A、B之间的距离,并请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
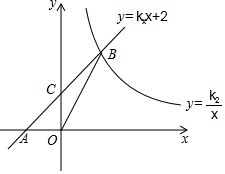 如图,在平面直角坐标系中,一次函数y=k1x+2的图象与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{{k}_{2}}{x}$的图象在第一象限内交于点B,连结BO.若S△OBC=1,tan∠BOC=$\frac{1}{3}$.
如图,在平面直角坐标系中,一次函数y=k1x+2的图象与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{{k}_{2}}{x}$的图象在第一象限内交于点B,连结BO.若S△OBC=1,tan∠BOC=$\frac{1}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com