
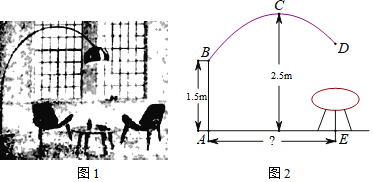
【题目】如图1是一款优雅且稳定的抛物线型落地灯,防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.86米,点最高点C距灯柱的水平距离为1.6米,灯柱AB及支架的相关数据如图2所示.若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为__米.
【答案】2.88.
【解析】
根据题意可以把AB所在的直线当作y轴,AE所在的直线当作x轴建立直角坐标系,由防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.86米,最高点C距灯柱的水平距离为1.6米,可以知道抛物线的顶点坐标C(1.6,2.5),直接设出顶点式y=a(x1.6)2+2.5,然后用待定系数法将(0,1.5)代入解析式解得a值,再将D点到地面的高当作纵坐标代入解析式即可求出AE的长,将不符合实际的取值舍去即可.
根据题意可以把AB所在的直线当作y轴,AE所在的直线当作x轴建立直角坐标系,
∴设y=a(x﹣1.6)2+2.5,
∴把x=0,y=1.5代入上式得,1.5=a(0﹣1.6)2+2.5,
解得:a=﹣![]() ,
,
∴y=﹣![]() (x﹣1.6)2+2.5,
(x﹣1.6)2+2.5,
又∵DE的高为1.86米,
∴当y=1.86时,则﹣![]() (x﹣1.6)2+2.5=1.86,
(x﹣1.6)2+2.5=1.86,
解得,x=2.88或x=0.32(舍去),
故答案为:2.88.


科目:初中数学 来源: 题型:
【题目】新型冠状病毒肺炎侵袭全国,全国人民团齐心协力共抗疫情。小明同学一直关注疫情的变化,期待疫情结束早日复课,他主要关注近一个月新增确诊病例和现有病例的情况,如图 1、图 2 所示,反映的是 2020 年 2 月 22 日至 3 月 23 日的新增确诊病例和现有病例的情况.
数据来源:疫情实时大数据报告
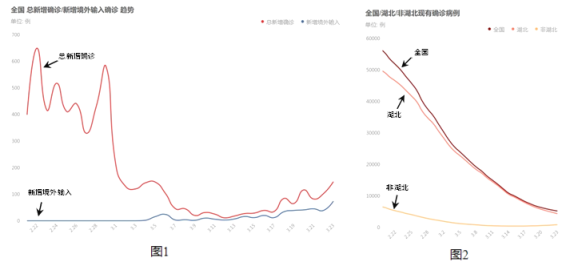
对近一个月内数据,下面有四个推断:
①全国新增境外输入病例呈上升趋势;
②全国一天内新增确诊人数最多约 650 人;
③全国新增确诊人数增加,现有确诊病例人数也增加;
④全国一日新增确诊人数的中位数约为 200. 所有合理推断的序号是( )
A.①②B.①②③C.②③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春天的某个周末,阳光明媚,适合户外运动.下午,住在同一小区的小懿、小静两人不约而同的都准备从小区出发,沿相同的路线步行去同一个公园赏花!小懿出发5分钟后小静才出发,同时小懿发现当天的光线很适合摄影,所以决定按原速回家拿相机,小懿拿了相机后,担心错过最佳拍照时间,所以速度提高了20%,结果还是比小静晚2分钟到公园.小懿取相机的时间忽略不计,在整个过程中,小静保持匀速运动,小懿提速前后也分别保持匀速运动.如图所示是小懿、小静之间的距离y(米)与小懿离开小区的时间x(分钟)之间的函数图象,则小区到公园的距离为_____米.
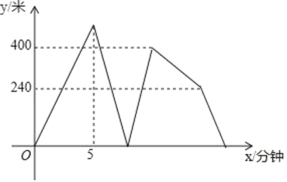
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 为
为![]() 边中点,动点
边中点,动点![]() 从点
从点![]() 出发,沿着
出发,沿着![]() 的路径以每秒1个单位长度的速度运动到
的路径以每秒1个单位长度的速度运动到![]() 点,在此过程中线段
点,在此过程中线段![]() 的长度
的长度![]() 随着运动时间
随着运动时间![]() 的函数关系如图2所示,则
的函数关系如图2所示,则![]() 的长为( )
的长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
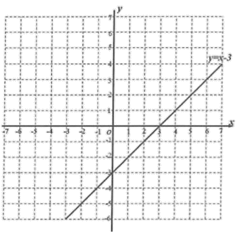
【题目】小聪对函数![]() 的图象和性质进行了探究.已知当自变量
的图象和性质进行了探究.已知当自变量![]() 的值为0或4时,函数值都为-3,当自变量
的值为0或4时,函数值都为-3,当自变量![]() 的值为-1或5时,函数值为2.
的值为-1或5时,函数值为2.
探究过程如下,请补充完整.
(1)这个函数的表达式为 ;
(2)在给出的平面直角坐标系中,画出这个函数的图象并写出这个函数的一条性质: ;
(3)进一步探究函数图象并解决问题:
①直线![]() 与函数
与函数![]() 有4个解,则k的取值范围为 ;
有4个解,则k的取值范围为 ;
②已知函数![]() 的图象如图所示,结合你所画的函数图象,写出不等式
的图象如图所示,结合你所画的函数图象,写出不等式![]() 的解集: .
的解集: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 和点
和点![]() 在抛物线
在抛物线![]() 上.
上.
(Ⅰ)求该抛物线的解析式和顶点坐标,并求出![]() 的值;
的值;
(Ⅱ)求点![]() 关于
关于![]() 轴对称点
轴对称点![]() 的坐标,并在
的坐标,并在![]() 轴上找一点
轴上找一点![]() ,使得
,使得![]() 最短,求此时点
最短,求此时点![]() 的坐标;
的坐标;
(Ⅲ)平移抛物线![]() ,记平移后点
,记平移后点![]() 的对应点为
的对应点为![]() ,点
,点![]() 的对应点为
的对应点为![]() ,点
,点![]() 是
是![]() 轴上的定点.
轴上的定点.
①当抛物线向左平移到某个位置时,![]() 最短,求此时抛物线的解析式;
最短,求此时抛物线的解析式;
②![]() 是
是![]() 轴上的定点,当抛物线向左平移到某个位置时,四边形
轴上的定点,当抛物线向左平移到某个位置时,四边形![]() 的周长最短,求此时抛物线的解析式(直接写出结果即可)
的周长最短,求此时抛物线的解析式(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
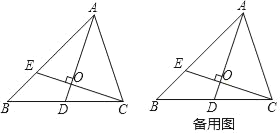
【题目】如图,△ABC中,D是边BC的中点,E是AB边上一点,且AD⊥CE于O,AD=AC=CE.
(1)求证:∠B=45°;
(2)求![]() 的值;
的值;
(3)直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
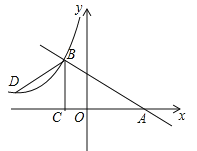
【题目】如图,已知一次函数y=kx+b的图象与x轴交于点A,与反比例函数![]() (x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.
(x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.
(1)求m的值;
(2)若∠DBC=∠ABC,求一次函数y=kx+b的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com