
ΓΨΧβΡΩΓΩ“―÷ΣœΏΕΈAB=30cm
(1)»γΆΦ1,ΒψP―ΊœΏΕΈABΉ‘ΒψAœρΒψB“‘2cm/sΒΡΥΌΕ»‘ΥΕ·,Ά§ ±ΒψQ―ΊœΏΕΈΒψBœρΒψA“‘3cm/sΒΡΥΌΕ»‘ΥΕ·,ΦΗΟκ÷”Κσ,PΓΔQΝΫΒψœύ”ω?
(2)»γΆΦ1,ΦΗΟκΚσ,ΒψPΓΔQΝΫΒψœύΨύ10cm?
(3)»γΆΦ2,AO=4cm,PO=2cm,Β±ΒψP‘ΎABΒΡ…œΖΫ,«“ΓœPOB=60Γψ ±,ΒψP»ΤΉ≈ΒψO“‘30Ε»/ΟκΒΡΥΌΕ»‘Ύ‘≤÷ή…œΡφ ±’κ–ΐΉΣ“Μ÷ήΆΘ÷Ι,Ά§ ±ΒψQ―Ί÷±œΏBAΉ‘BΒψœρAΒψ‘ΥΕ·,ΦΌ»τΒψPΓΔQΝΫΒψΡήœύ”ω,«σΒψQΒΡ‘ΥΕ·ΥΌΕ».
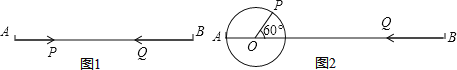
ΓΨ¥πΑΗΓΩΘ®1Θ©6sΘΜΘ®2Θ©4sΜρ8sΘΜΘ®3Θ©7cm/sΜρ2.4cm/s
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΗυΨίœύ”ω ±Θ§ΒψPΚΆΒψQΒΡ‘ΥΕ·ΒΡ¬Ζ≥ΧΚΆΒ»”ΎABΒΡ≥ΛΝ–ΖΫ≥ΧΦ¥Ω…«σΫβΘΜ
Θ®2Θ©…ηΨ≠ΙΐxsΘ§PΓΔQΝΫΒψœύΨύ10cmΘ§Ζ÷œύ”ω«ΑΚΆœύ”ωΚσΝΫ÷÷«ιΩωΫ®ΝΔΖΫ≥Χ«σ≥ωΤδΫβΦ¥Ω…ΘΜ
Θ®3Θ©”…”ΎΒψPΘ§Q÷ΜΡή‘Ύ÷±œΏAB…œœύ”ωΘ§ΕχΒψP–ΐΉΣΒΫ÷±œΏAB…œΒΡ ±ΦδΖ÷2÷÷«ιΩωΘ§Υυ“‘ΗυΨίΧβ“βΝ–≥ωΖΫ≥ΧΖ÷±π«σΫβΘ°
‘ΧβΫβΈωΘΚΘ®1Θ©…ηΨ≠ΙΐtsΚσΘ§ΒψPΓΔQœύ”ωΘ°
“άΧβ“βΘ§”–2t+3t=30Θ§
ΫβΒΟΘΚt=6Θ°
¥πΘΚΨ≠Ιΐ6Οκ÷”ΚσΘ§ΒψPΓΔQœύ”ωΘΜ
Θ®2Θ©…ηΨ≠ΙΐxsΘ§PΓΔQΝΫΒψœύΨύ10cmΘ§”…Χβ“βΒΟ
2x+3x+10=30Μρ2x+3x©¹10=30Θ§
ΫβΒΟΘΚx=4Μρx=8Θ°
¥πΘΚΨ≠Ιΐ4Οκ÷”Μρ8Οκ÷”ΚσΘ§PΓΔQΝΫΒψœύΨύ10cmΘΜ
Θ®3Θ©ΒψPΘ§Q÷ΜΡή‘Ύ÷±œΏAB…œœύ”ωΘ§
‘ρΒψP–ΐΉΣΒΫ÷±œΏAB…œΒΡ ±ΦδΈΣ![]() = 4Θ®sΘ©Μρ
= 4Θ®sΘ©Μρ![]() =10Θ®sΘ©Θ°
=10Θ®sΘ©Θ°
…ηΒψQΒΡΥΌΕ»ΈΣycm/sΘ§‘ρ”–4y=30 - 2Θ§ΫβΒΟ y=7ΘΜ
Μρ10y=30©¹6Θ§ΫβΒΟy=2.4ΘΜ
¥πΘΚΒψPΒΡΥΌΕ»ΈΣ7cm/sΜρ2.4cm/sΘ°


 Ϋρ«≈ΫΧ”ΐΦΤΥψ–ΓΉ¥‘ΣœΒΝ–¥πΑΗ
Ϋρ«≈ΫΧ”ΐΦΤΥψ–ΓΉ¥‘ΣœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓœAFD=Γœ1Θ§ACΓΈDEΘ°
(1) ‘ΥΒΟςΘΚDFΓΈBCΘΜ
(2)»τΓœ1=68ΓψΘ§DFΤΫΖ÷ΓœADEΘ§«σΓœBΒΡΕ» ΐΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ΜΕά÷Ι»ΈΣΜΊάΓΙψ¥σΙ»Ο‘Θ§‘Ύ νΦΌΤΎΦδΆΤ≥ω―ß…ζΗω»ΥΟ≈Τ±”≈ΜίΦέΘ§ΗςΤ±Φέ»γœ¬ΘΚ
Τ±Φέ÷÷άύ | Θ®AΘ©―ß…ζ“Ι≥ΓΤ± | Θ®BΘ©―ß…ζ»’Ά®Τ± | Θ®CΘ©ΫΎΦΌ»’Ά®Τ± |
ΒΞΦέΘ®‘ΣΘ© | 80 | 120 | 150 |
Ρ≥¥»…ΤΒΞΈΜ”ϊΙΚ¬ρ»ΐ÷÷άύ–ΆΒΡΤ±Ι≤100’≈Ϋ±άχΤΖ―ßΦφ”≈ΒΡΝτ Ί―ß…ζΘ§Τδ÷–ΙΚ¬ρΒΡB÷÷Τ± ΐ «A÷÷Τ± ΐΒΡ3±ΕΜΙΕύ7’≈Θ§…ηΙΚ¬ρA÷÷Τ±x’≈Θ§C÷÷Τ±y’≈Θ°
Θ®1Θ©÷±Ϋ”–¥≥ωx”κy÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®2Θ©…ηΙΚΤ±ΉήΖ―”ΟΈΣW‘ΣΘ§«σWΘ®‘ΣΘ©”κxΘ®’≈Θ©÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®3Θ©ΈΣΖΫ±ψ―ß…ζ”ΈΆφΘ§ΦΤΜ°ΙΚ¬ρΒΡ―ß…ζ“Ι≥ΓΤ±≤ΜΒΆ”Ύ20’≈Θ§«“ΟΩ÷÷Τ±÷Ν…ΌΙΚ¬ρ5’≈Θ§‘ρ”–ΦΗ÷÷ΙΚΤ±ΖΫΑΗΘΩ≤Δ÷Η≥ωΡΡ÷÷ΖΫΑΗΖ―”ΟΉν…ΌΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΙΊ”ΎxΒΡΖΫ≥Χx2©¹Θ®m+2Θ©x+2mΘΫ0Θ°
Θ®1Θ©»τΗΟΖΫ≥ΧΒΡ“ΜΗωΗυΈΣxΘΫ1Θ§«σmΒΡ÷ΒΘΜ
Θ®2Θ©«σ÷ΛΘΚ≤Μ¬έm»ΓΚΈ Β ΐΘ§ΗΟΖΫ≥ΧΉή”–ΝΫΗω Β ΐΗυΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ2011ΡξΘ§Έ“ΙζΤϊ≥ΒœζΝΩ≥§ΙΐΝΥ18500000ΝΨΘ§’βΗω ΐΨί”ΟΩΤ―ßΦ« ΐΖ®±μ ΨΈΣ
ΓΓ Γχ ΓΓΝΨΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν– ¬Φΰ÷– «ΥφΜζ ¬ΦΰΒΡΗω ΐ «Θ®ΓΓΓΓΘ©
ΔΌΆΕ÷ά“ΜΟΕ”≤±“Θ§’ΐΟφ≥·…œΘΜ
ΔΎΈε±Ώ–ΈΒΡΡΎΫ«ΚΆ «540ΓψΘΜ
Δέ20Φΰ≤ζΤΖ÷–”–5Φΰ¥ΈΤΖΘ§¥”÷–»Έ“β≥ι»Γ6ΦΰΘ§÷Ν…Ό”–“ΜΦΰ «¥ΈΤΖΘΜ
Δή“ΜΗωΆΦ–ΈΤΫ“ΤΚσ”κ‘≠ά¥ΒΡΆΦ–Έ≤Μ»ΪΒ»Θ°
A.0B.1C.2D.3
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΨΊ–ΈABCD÷–Θ§AB=3Θ§BC=4Θ§ΒψE «BC±Ώ…œ“ΜΒψΘ§Ν§Ϋ”AEΘ§Α―ΓœB―ΊAE’έΒΰΘ§ ΙΒψB¬δ‘ΎΒψBΓδ¥ΠΘ°Β±ΓςCEBΓδΈΣ÷±Ϋ«»ΐΫ«–Έ ±Θ§BEΒΡ≥ΛΈΣ Θ° 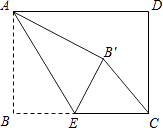
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΒψC‘Ύx÷α…œΖΫΘ§y÷αΉσ≤ύΘ§Ψύάκx÷α2ΗωΒΞΈΜΘ§Ψύάκy÷α3ΗωΒΞΈΜΘ§‘ρΒψCΒΡΉχ±ξΈΣ(ΓΓΓΓ)
A. (2Θ§3) B. (Θ≠2Θ§Θ≠3) C. (Θ≠3Θ§2) D. (3Θ§Θ≠2)
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΡΕΝœ¬Ν–≤ΡΝœΘΚ
ΓΕ’≈«πΫ®ΥψΨ≠ΓΖ «“Μ≤Ω ΐ―ßΈ ΧβΦ·Θ§ΤδΡΎ»ίΓΔΖΕΈß”κΓΕΨ≈’¬Υψ θΓΖœύΖ¬Θ°Τδ÷–Χα≥ω≤ΔΫβΨωΝΥ“ΜΗω‘Ύ ΐ―ß Ζ…œΖ«≥Θ÷χΟϊΒΡ≤ΜΕ®ΖΫ≥ΧΈ ΧβΘ§Ά®≥Θ≥ΤΈΣΓΑΑΌΦΠΈ ΧβΓ±ΘΚΓΑΫώ”–ΦΠΈΧ“Μ÷Β«°ΈεΘ§ΦΠΡΗ“Μ÷Β«°»ΐΘ§ΦΠ≥ϊ»ΐ÷Β«°“ΜΘ°Ζ≤ΑΌ«°¬ρΦΠΑΌ÷ΜΘ§Έ ΦΠΈΧΓΔΡΗΓΔ≥ϊΗςΦΗΚΈΘ°Γ±
“κΈΡΘΚΟΩ“Μ÷ΜΙΪΦΠ÷ΒΈεΈΡ«°Θ§ΟΩ“Μ÷ΜΡΗΦΠ÷Β»ΐΈΡ«°Θ§ΟΩ»ΐ÷Μ–ΓΦΠ÷Β“ΜΈΡ«°Θ°œ÷‘Ύ”Ο“ΜΑΌΈΡ«°¬ρ“ΜΑΌ÷ΜΦΠΘ§Έ ’β“ΜΑΌ÷ΜΦΠ÷–Θ§ΙΪΦΠΓΔΡΗΦΠΓΔ–ΓΦΠΗς”–Εύ…Ό÷ΜΘΩ
ΫαΚœΡψ―ßΙΐΒΡ÷Σ ΕΘ§ΫβΨωœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©»τ…ηΡΗΦΠ”–x÷ΜΘ§ΙΪΦΠ”–y÷ΜΘ§
ΔΌ –ΓΦΠ”–__________÷ΜΘ§¬ρ–ΓΦΠ“ΜΙ≤Μ®Ζ―__________ΈΡ«°ΘΜΘ®”ΟΚ§xΘ§yΒΡ ΫΉ”±μ ΨΘ©
ΔΎΗυΨίΧβ“βΘ§Ν–≥ω“ΜΗωΚ§”–xΘ§yΒΡΖΫ≥ΧΘΚ__________________ΘΜ
Θ®2Θ©»τΕ‘ΓΑΑΌΦΠΈ ΧβΓ±‘ωΦ”“ΜΗωΧθΦΰΘΚΡΗΦΠ ΐΝΩ «ΙΪΦΠ ΐΝΩΒΡ4±ΕΕύ2÷ΜΘ§«σ¥Υ ±ΙΪΦΠΓΔΡΗΦΠΓΔ–ΓΦΠΗς”–Εύ…Ό÷Μ?
Θ®3Θ©≥ΐΝΥΈ ΧβΘ®2Θ©÷–ΒΡΫβ÷°ΆβΘ§«κΡψ‘Ό÷±Ϋ”–¥≥ωΝΫΉιΖϊΚœΓΑΑΌΦΠΈ ΧβΓ±ΒΡΫβΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com