
����Ŀ��ij���ֹ�Ϊ���������ԣ�������ڼ��Ƴ�ѧ��������Ʊ�Żݼۣ���Ʊ�����£�
Ʊ������ | ��A��ѧ��ҹ��Ʊ | ��B��ѧ����ͨƱ | ��C���ڼ���ͨƱ |
���ۣ�Ԫ�� | 80 | 120 | 150 |
ij���Ƶ�λ�������������͵�Ʊ��100�Ž���Ʒѧ���ŵ�����ѧ�������й����B��Ʊ����A��Ʊ����3������7�ţ��蹺��A��Ʊx�ţ�C��Ʊy�ţ�
��1��ֱ��д��x��y֮��ĺ�����ϵʽ��
��2���蹺Ʊ�ܷ���ΪWԪ����W��Ԫ����x���ţ�֮��ĺ�����ϵʽ��
��3��Ϊ����ѧ�����棬�ƻ������ѧ��ҹ��Ʊ������20�ţ���ÿ��Ʊ���ٹ���5�ţ����м��ֹ�Ʊ��������ָ�����ַ����������٣�
���𰸡�
��1���⣺x+3x+7+y=100��
����y=93��4x
��2���⣺w=80x+120��3x+7��+150��93��4x��
=��160x+14790
��3���⣺�������  ��
��
���20��x��22��
��Ϊ����xΪ20��21��22��
���Թ���3�ֹ�Ʊ������A��20��B��67��C��13��A��21��B��70��C��9��A��22��B��73��C��5����
��w=��160x+14790��
��Ϊk=��160��0��
����y��x�����������
���Ե�x=22ʱ��y��С=22������160��+14790=11270��
����A��ƱΪ22�ţ�B��Ʊ73�ţ�C��ƱΪ5��ʱ�������٣����ٷ���Ϊ11270Ԫ
����������1��������Ʊ��Ϊ100�õ�x+3x+7+y=100��Ȼ����x��ʾy���ɣ���2�����ñ������ݰ�����Ʊ�ķ��ü������õ�w=80x+120��3x+7��+150��93��4x����Ȼ���������ɣ���3����������õ�  ���ٽⲻ��ʽ����ȷ������ʽ���������Ϊ20��21��22�����ǵõ�����3�ֹ�Ʊ������Ȼ�����һ�κ�����������w����Сֵ��
���ٽⲻ��ʽ����ȷ������ʽ���������Ϊ20��21��22�����ǵõ�����3�ֹ�Ʊ������Ȼ�����һ�κ�����������w����Сֵ��
�����㾫�����������⣬������Ҫ�˽�һԪһ�β���ʽ���Ӧ��(1���������⣬�ҳ����ȹ�ϵ��2���裺��δ֪����3���У��г�����ʽ�飻4���⣺�ⲻ��ʽ�飻5�����飺�Ӳ���ʽ��Ľ⼯���ҳ���������Ĵ𰸣�6����д�������)��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��CΪ��Բ��һ�㣬OΪԲ�ģ�ֱ��AB��Ϊ2cm����BOC=60�㣬��BCO=90��������BOC��Բ��O��ʱ����ת����B��OC������C����OA�ϣ����BCɨ������ͼ����Ӱ���֣������Ϊ_______cm2��
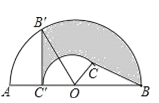
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijˮ�����ϰ���ÿ��xԪ�ĵ��۹�����ݮ100��Ӽ�30%����70���Ժ�ÿ��Ƚ��۽���aԪ����ʣ��30��ȫ����������ɻ������Ϊ________Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l1�Ľ���ʽΪy=��3x+3����l1��x�ύ�ڵ�D��ֱ��l2������A��B��ֱ��l1 �� l2���ڵ�C�� 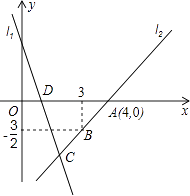
��1����ֱ��l2�Ľ�������ʽ��
��2�����ADC�������
��3������PΪ��һ�����ϵ�һ�㣬����A��C��D��PΪ������ı���Ϊƽ���ı��Σ������P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�߶�AB=30cm
(1)��ͼ1,��P���߶�AB�Ե�A���B��2cm/s���ٶ��˶�,ͬʱ��Q���߶ε�B���A��3cm/s���ٶ��˶�,�����Ӻ�,P��Q��������?
(2)��ͼ1,�����,��P��Q�������10cm?
(3)��ͼ2,AO=4cm,PO=2cm,����P��AB���Ϸ�,�ҡ�POB=60��ʱ,��P���ŵ�O��30��/����ٶ���Բ������ʱ����תһ��ֹͣ,ͬʱ��Q��ֱ��BA��B����A���˶�,������P��Q����������,���Q���˶��ٶ�.
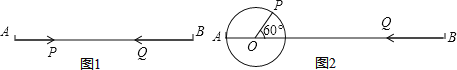
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ֱ������ABCD�У�AD��BC����A=90�㣬AB=12��BC=21��AD=16������P�ӵ�B������������BC�ķ�����ÿ��2����λ�����ٶ��˶�������Qͬʱ�ӵ�A���������߶�AD����ÿ��1����λ�����ٶ����D�˶���������һ�����㵽��˵�ʱ��һ������Ҳ��ֹ֮ͣ�˶������˶���ʱ��Ϊt���룩�� 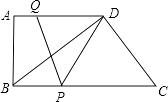
��1�����DPQ�����ΪS����S��t֮��ĺ�����ϵʽ��
��2����tΪ��ֵʱ���ı���PCDQ��ƽ���ı��Σ�
��3���ֱ������tΪ��ֵʱ����PD=PQ����DQ=PQ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com