
【题目】如图,直线l1的解析式为y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1 , l2交于点C. 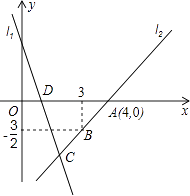
(1)求直线l2的解析表达式;
(2)求△ADC的面积;
(3)若点P为第一象限上的一点,且以A,C,D,P为顶点的四边形为平行四边形,试求点P的坐标.
【答案】
(1)解:设直线l2的解析表达式为y=kx+b,
则有  ,
,
解得 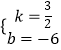 .
.
故直线l2的解析表达式是y= ![]() x﹣6
x﹣6
(2)解:由 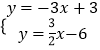 得
得 ![]() ,
,
所以点C坐标为(2,﹣3),
则D点的坐标为(1,0),
AD=3,
过点C作x轴的垂线,垂足为E,则CE=|﹣3|=3,
因此S△ADC= ![]() ×3×3=4.5
×3×3=4.5
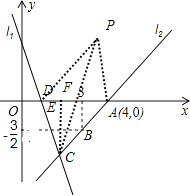
(3)解:如图,设P(m,n),AD与CP的交点为F,
∵四边形ACDP为平行四边形
∴PF=PC,DF=FA
∵AD=3,
∴F(2.5,0)
∵C(2,﹣3)
由中点坐标公式得m+2=2.5×2,n+(﹣3)=0×2,
∴m=3,n=3,
∴P(3,3).
【解析】(1)设出直线l2的解析表达式,代入直线上的两点求得答案即可;(2)求得两条直线的交点坐标,以及点D的坐标,进一步利用三角形的面积计算方法得出答案即可;(3)利用平行四边形的性质以及中点坐标的求法得出答案即可.


 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程kx2+2x﹣1=0有实数根,则实数k的取值范围是( )
A. k≥﹣1 B. k>﹣1 C. k≥﹣1且k≠0 D. k≠0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某欢乐谷为回馈广大谷迷,在暑假期间推出学生个人门票优惠价,各票价如下:
票价种类 | (A)学生夜场票 | (B)学生日通票 | (C)节假日通票 |
单价(元) | 80 | 120 | 150 |
某慈善单位欲购买三种类型的票共100张奖励品学兼优的留守学生,其中购买的B种票数是A种票数的3倍还多7张,设购买A种票x张,C种票y张.
(1)直接写出x与y之间的函数关系式;
(2)设购票总费用为W元,求W(元)与x(张)之间的函数关系式;
(3)为方便学生游玩,计划购买的学生夜场票不低于20张,且每种票至少购买5张,则有几种购票方案?并指出哪种方案费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为 . 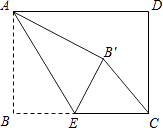
查看答案和解析>>
科目:初中数学 来源: 题型:
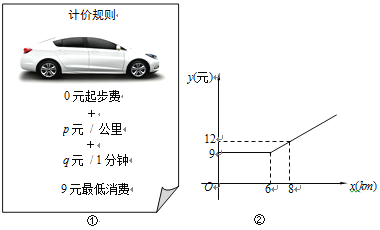
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎.该打车方式的计价规则如图①所示,若车辆以平均速度vkm/h行驶了skm,则打车费用为(ps+60q·![]() )元(不足9元按9元计价).小明某天用该打车方式出行,按上述计价规则,其打车费用y(元)与行驶里程x(km)的函数关系也可由如图②表示.
)元(不足9元按9元计价).小明某天用该打车方式出行,按上述计价规则,其打车费用y(元)与行驶里程x(km)的函数关系也可由如图②表示.
(1)当x≥6时,求y与x的函数关系式.
(2)若p=1,q=0.5,求该车行驶的平均速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com