
【题目】阅读下列材料:
《张丘建算经》是一部数学问题集,其内容、范围与《九章算术》相仿.其中提出并解决了一个在数学史上非常著名的不定方程问题,通常称为“百鸡问题”:“今有鸡翁一值钱五,鸡母一值钱三,鸡雏三值钱一.凡百钱买鸡百只,问鸡翁、母、雏各几何.”
译文:每一只公鸡值五文钱,每一只母鸡值三文钱,每三只小鸡值一文钱.现在用一百文钱买一百只鸡,问这一百只鸡中,公鸡、母鸡、小鸡各有多少只?
结合你学过的知识,解决下列问题:
(1)若设母鸡有x只,公鸡有y只,
① 小鸡有__________只,买小鸡一共花费__________文钱;(用含x,y的式子表示)
②根据题意,列出一个含有x,y的方程:__________________;
(2)若对“百鸡问题”增加一个条件:母鸡数量是公鸡数量的4倍多2只,求此时公鸡、母鸡、小鸡各有多少只?
(3)除了问题(2)中的解之外,请你再直接写出两组符合“百鸡问题”的解.
【答案】解:(1)①![]() ,
, ![]() ;②
;②![]() ;(2)母鸡有18只,公鸡有4只,小鸡有78只.(3)以下三组答案,写出其中任意两组即可:①公鸡有12只,母鸡有4只,小鸡有84只;②公鸡有8只,母鸡有11只,小鸡有81只;③公鸡有0只,母鸡有25只,小鸡有75只.
;(2)母鸡有18只,公鸡有4只,小鸡有78只.(3)以下三组答案,写出其中任意两组即可:①公鸡有12只,母鸡有4只,小鸡有84只;②公鸡有8只,母鸡有11只,小鸡有81只;③公鸡有0只,母鸡有25只,小鸡有75只.
【解析】试题分析:(1)设母鸡有x只,公鸡有y只,根据一百文钱买一百只鸡,表示出小鸡的数量和价钱,然后列出方程;
(2)设母鸡有x只,公鸡有y只,根据根据一百文钱买一百只鸡,母鸡数量是公鸡数量的4倍多2只,列方程求解即可;
(3)解不定方程即可.
试题解析:解:(1)①![]() ,
, ![]() ;②
;② ![]() ;
;
(2)设母鸡有x只,公鸡有y只,根据题意,得:
![]() ,解得
,解得![]() ,
, ![]() (只),
(只),
答:母鸡有18只,公鸡有4只,小鸡有78只.
(3)以下三组答案,写出其中任意两组即可:
①公鸡有12只,母鸡有4只,小鸡有84只;
②公鸡有8只,母鸡有11只,小鸡有81只;
③公鸡有0只,母鸡有25只,小鸡有75只.


科目:初中数学 来源: 题型:
【题目】已知线段AB=30cm
(1)如图1,点P沿线段AB自点A向点B以2cm/s的速度运动,同时点Q沿线段点B向点A以3cm/s的速度运动,几秒钟后,P、Q两点相遇?
(2)如图1,几秒后,点P、Q两点相距10cm?
(3)如图2,AO=4cm,PO=2cm,当点P在AB的上方,且∠POB=60°时,点P绕着点O以30度/秒的速度在圆周上逆时针旋转一周停止,同时点Q沿直线BA自B点向A点运动,假若点P、Q两点能相遇,求点Q的运动速度.
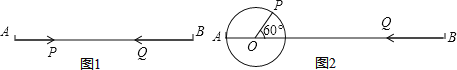
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在直角梯形ABCD中,AD∥BC,∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒). 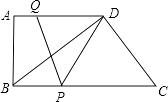
(1)设△DPQ的面积为S,求S与t之间的函数关系式;
(2)当t为何值时,四边形PCDQ是平行四边形?
(3)分别求出当t为何值时,①PD=PQ,②DQ=PQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A. 垂直于同一直线的两条直线平行
B. 有两边和其中一边上的高对应相等的两个三角形全等
C. 三角形三个内角中,至少有2个锐角
D. 有两条边和一个角对应相等的两个三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某股票市场,买、卖股票都要分别交纳印花税等有关税费.以A市股的股票交易为例,除成本外还要交纳:
①印花税:按成交金额的0.1%计算;
②过户费:按成交金额的0.1%计算;
③佣金:按不高于成交金额的0.3%计算(本题按0.3%计算),不足5元按5元计算,
例:某投资者以每股5.00元的价格在沪市A股中买入股票“金杯汽车”1000股,以每股5.50元的价格全部卖出,共盈利多少?
解:直接成本:5×1000=5000(元);
印花税:(5000+5.50×1000)×0.1%=10.50(元);
过户费:(5000+5.50×1000)×0.1%=10.50(元);
佣金:5000×0.3%=15.00(元) 5.50×1000×0.3%=16.50(元)
∵15.00>5 16.50>5 ∴佣金为15.00+16.50=31.50元.
总支出:5000+10.50+10.50+31.50=5052.50(元);
总收入:5.50×1000=5500(元);
总盈利:5500-5052.50=447.50(元).
问题:
(1)小王对此很感兴趣,以每股5.00元的价格买入以上股票100股,以每股5.50元的价格全部卖出,则他盈利为______________元;
(2)小张以每股a(a≥5)元的价格买入以上股票1000股,股市波动大,他准备在不亏不盈时卖出.请你帮他计算出卖出的价格每股是多少元(用a的代数式表示)?
(3)小张再以每股5.00元的价格买入以上股票1000股,准备盈利1000元时才卖出,请你帮他计算卖出的价格每股是多少元?(精确到0.01元)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣11,点B表示10,点C表示18,我们称点A和点C在数轴上相距29个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.

问:(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com