
【题目】如图,直线y=﹣x+3与x轴,y轴分别相交于点B、点C,经过B、C两点的抛物线y=ax2+bx+c与x轴的另一交点为A,点A在点B的左边,顶点为P,且线段AB的长为2.
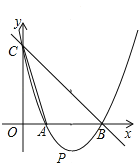
(1)求点A的坐标;
(2)求该抛物线的函数表达式;
(3)在抛物线的对称轴上是否存在点G,使|GC﹣GB|最大?若存在,求G点坐标;若不存在说明理由.
(4)连结AC,请问在x轴上是否存在点Q,使得以点P,B,Q为顶点的三角形与△ABC相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
【答案】(1)(1,0);(2)y=x2﹣4x+3;(3)G点坐标为(2,﹣3);(4)在x轴上存在两点Q1(0,0),Q2(![]() ,0)
,0)
【解析】
试题分析:(1)求值直线y=﹣x+3与x轴的交点B,然后根据AB的长,即可求得OA的长,则A的坐标即可求得;
(2)利用待定系数法求得二次函数的解析式;
(3)由于A、B两点关于抛物线的对称轴即直线x=2对称,所以G点为直线CA与直线x=2的交点,先运用待定系数法求出直线AC的解析式,再令x=2,求出y的值,进而得出G点坐标;
(4)分成![]() =
=![]() ,∠PBQ=∠ABC=45°和
,∠PBQ=∠ABC=45°和![]() =
=![]() ,∠QBP=∠ABC=45°两种情况求得QB的长,据此即可求解.
,∠QBP=∠ABC=45°两种情况求得QB的长,据此即可求解.
解:(1)当y=0时,﹣x+3=0,解得x=3,即B(3,0),
由AB=2,得3﹣2=1,
A的坐标为(1,0);
(2)根据题意得: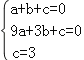 ,
,
解得: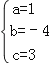 ,
,
则抛物线的解析式是:y=x2﹣4x+3;
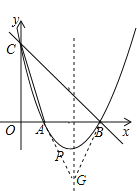
(3)延长CA,交对称轴于点G,连接GB,则|GC﹣GB|=GC﹣GA=AC最大.
∵抛物线y=x2﹣4x+3与x轴交于点A、点B(3,0),且对称轴为直线x=2,
∴点A的坐标为(1,0).
设直线AC的解析式为y=kx+m,
∵A(1,0),C(0,3),
∴![]() ,
,
解得![]() ,
,
∴y=﹣3x+3,
当x=2时,y=﹣3×2+3=﹣3,
∴G点坐标为(2,﹣3);
(4)①当![]() =
=![]() ,∠PBQ=∠ABC=45°时,△PBQ∽△ABC.
,∠PBQ=∠ABC=45°时,△PBQ∽△ABC.
即![]() =
=![]()
∴BQ=3,
又∵BO=3,
∴点Q与点O重合,
∴Q1的坐标是(0,0).
②当![]() =
=![]() ,∠QBP=∠ABC=45°时,△QBP∽△ABC.
,∠QBP=∠ABC=45°时,△QBP∽△ABC.
即![]() =
=![]() ,
,
QB=![]() .
.
∵OB=3,
∴OQ=OB﹣QB=3﹣![]() =
=![]()
∴Q2的坐标是(![]() ,0).
,0).
∵∠PBx=180°﹣45°=135°,∠BAC<135°,
∴∠PBx≠∠BAC.
∴点Q不可能在B点右侧的x轴上
综上所述,在x轴上存在两点Q1(0,0),Q2(![]() ,0)
,0)


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
①a、b同号;
②当x=1和x=3时,函数值相等;
③4a+b=0;
④当y=﹣2时,x的值只能取0.
其中正确的个数是( )
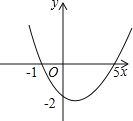
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
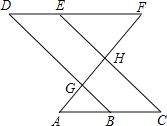
【题目】如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D.
则∠A=∠F,请说明理由.
解:∵∠AGB=∠EHF
∠AGB= (对顶角相等)
∴∠EHF=∠DGF
∴DB∥EC
∴∠ =∠DBA ( 两直线平行,同位角相等)
又∵∠C=∠D
∴∠DBA=∠D
∴DF∥ (内错角相等,两直线平行)
∴∠A=∠F .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥DE,AC∥DF,AC=DF,下列条件中不能判断△ABC≌△DEF的是( )
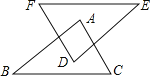
A.AB=DE B.∠B=∠E C.EF=BC D.EF∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
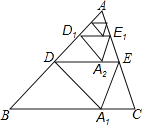
【题目】如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2016次操作后得到的折痕D2015E2015到BC的距离记为h2016,到BC的距离记为h2016.若h1=1,则h2016的值为( )
A.![]() B.1﹣
B.1﹣![]() C.
C.![]() D.2﹣
D.2﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钓鱼岛是我国渤海海峡上的一颗明珠,渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后,发现一外国舰艇进入我国水域向钓鱼岛驶来,渔船向渔政部门报告,并立即返航.渔政船接到报告后,立即从该港口出发赶往钓鱼岛.下图是渔船及渔政船与港口的距离s和渔船离开港口的时间t之间的函数图象.(假设渔船与渔政船沿同一航线航行)

(1)直接写出渔船离港口的距离s和它离开港口的时间t的函数关系式.]
(2)求渔船和渔政船相遇时,两船与钓鱼岛的距离.
(3)在渔政船驶往钓鱼岛的过程中,求渔船从港口出发经过多长时间与渔政船相距30海里?
查看答案和解析>>
科目:初中数学 来源: 题型:
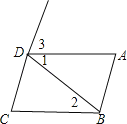
【题目】推理填空:如图:
①若∠1=∠2,
则 ∥ (内错角相等,两直线平行);
若∠DAB+∠ABC=180°,
则 ∥ (同旁内角互补,两直线平行);
②当 ∥ 时,
∠C+∠ABC=180°(两直线平行,同旁内角互补);
③当 ∥ 时,
∠3=∠C (两直线平行,同位角相等).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com