
【题目】如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D.
则∠A=∠F,请说明理由.
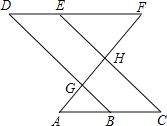
解:∵∠AGB=∠EHF
∠AGB= (对顶角相等)
∴∠EHF=∠DGF
∴DB∥EC
∴∠ =∠DBA ( 两直线平行,同位角相等)
又∵∠C=∠D
∴∠DBA=∠D
∴DF∥ (内错角相等,两直线平行)
∴∠A=∠F .
【答案】已知;∠DGF;同位角相等,两直线平行;C;AC;两直线平行,内错角相等
【解析】
试题分析:根据对顶角相等推知同位角∠EHF=∠DGF,从而证得两直线DB∥EC;然后由平行线的性质知内错角∠DBA=∠D,即可根据平行线的判定定理推知两直线DF∥AC;最后由平行线的性质(两直线平行,内错角相等)证得∠A=∠F.
解:∵∠AGB=∠EHF(已知),∠AGB=∠DGF(对顶角相等),
∴∠EHF=∠DGF
∴DB∥EC(同位角相等,两直线平行),
∴∠C=∠DBA ( 两直线平行,同位角相等);
又∵∠C=∠D(已知),
∴∠DBA=∠D(等量代换),
∴DF∥AC(内错角相等,两直线平行),
∴∠A=∠F(两直线平行,内错角相等);
故答案是:已知;∠DGF;同位角相等,两直线平行;C;AC;两直线平行,内错角相等.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】扬州某楼盘准备以每平方米的10000元均价销售,经过两次下调后,决定以每平方米8600元的均价开盘.若设平均每次下调的百分率为x,则可列方程________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=a3-2ab2+1,B=a3+ab2-3a2b,则A+B=( ).
A. 2a3-3ab2-3a2b+1 B. 2a3+ab2-3a2b+1
C. 2a3+ab2-3a2b+1 D. 2a3-ab2-3a2b+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+3与x轴,y轴分别相交于点B、点C,经过B、C两点的抛物线y=ax2+bx+c与x轴的另一交点为A,点A在点B的左边,顶点为P,且线段AB的长为2.
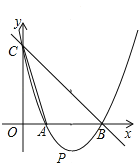
(1)求点A的坐标;
(2)求该抛物线的函数表达式;
(3)在抛物线的对称轴上是否存在点G,使|GC﹣GB|最大?若存在,求G点坐标;若不存在说明理由.
(4)连结AC,请问在x轴上是否存在点Q,使得以点P,B,Q为顶点的三角形与△ABC相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com