练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知A＝a3－2ab2＋1，B＝a3＋ab2－3a2b，则A＋B＝( )．

    A. 2a3－3ab2－3a2b＋1 B. 2a3＋ab2－3a2b＋1

    C. 2a3＋ab2－3a2b＋1 D. 2a3－ab2－3a2b＋1

    【答案】D

    【解析】根据整式的加减法法则“几个整式相加减，如果有括号就先去括号，然后再合并同类项”进行计算即可得出答案.

    解：A＋B＝(a3－2ab2＋1)＋(a3＋ab2－3a2b)

    ＝a3－2ab2＋1＋a3＋ab2－3a2b

    ＝2a3－ab2－3a2b＋1.

    故选D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知A、B两地相距40千米，中午12：00时，甲从A地出发开车到B地，12：10时乙从B地出发骑自行车到A地，设甲行驶的时间为t（分），甲、乙两人离A地的距离S（千米）与时间t（分）之间的关系如图所示．由图中的信息可知，乙到达A地的时间为（ ）

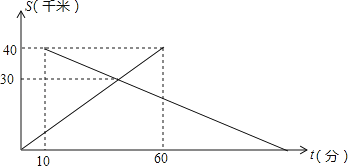
    A．14：00 B．14：20 C．14：30 D．14：40

    查看答案和解析>>

    科目：初中数学 来源： 题型：

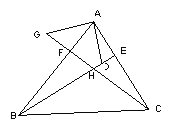
    【题目】如图：在△ABC中，BE、CF分别是AC、AB两边上的高，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连结AD、AG。

    求证：（1）AD=AG，（2）AD与AG的位置关系如何。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论：

    ①a、b同号；

    ②当x=1和x=3时，函数值相等；

    ③4a+b=0；

    ④当y=﹣2时，x的值只能取0．

    其中正确的个数是（ ）

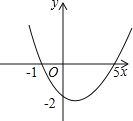
    A．1个 B．2个 C．3个 D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列图形中，对称轴有且只有3条的是（ ）

    A. 菱形 B. 等边三角形 C. 正方形 D. 圆

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图， AD=CD=CB=AB=a，DA∥CB，AB⊥CB，∠BAC的平分线交BC于E，作EF⊥AC于F，作FG⊥AB于G．

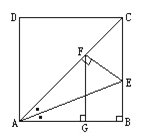
    （1）求AC的长；（2）求证：AB=AG.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】平行四边形、矩形、菱形、等腰三角形、正方形中是轴对称图形的有（）个

    A、1 B、2 C、3 D、4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点E在直线DF上，点B在直线AC上，若∠AGB=∠EHF，∠C=∠D．

    则∠A=∠F，请说明理由．

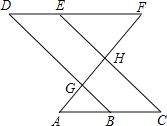
    解：∵∠AGB=∠EHF

    ∠AGB= （对顶角相等）

    ∴∠EHF=∠DGF

    ∴DB∥EC

    ∴∠ =∠DBA （ 两直线平行，同位角相等）

    又∵∠C=∠D

    ∴∠DBA=∠D

    ∴DF∥ （内错角相等，两直线平行）

    ∴∠A=∠F ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图直线AB、CD、EF相交于点O，是∠AOC的邻补角是 ，∠DOA的对顶角是 ，若∠AOC=50°，则∠BOD= 度，∠COB= 度．

    查看答案和解析>>

    同步练习册答案