
 现有一个“Z”型的工件(工件厚度忽略不计),如图示,其中AB为20cm,BC为60cm,∠ABC=90°,∠BCD=50°,求该工件如图摆放时的高度(即A到CD的距离).
现有一个“Z”型的工件(工件厚度忽略不计),如图示,其中AB为20cm,BC为60cm,∠ABC=90°,∠BCD=50°,求该工件如图摆放时的高度(即A到CD的距离).分析 过点A作AP⊥CD于点P,交BC于点Q,由∠CQP=∠AQB、∠CPQ=∠B=90°知∠A=∠C=50°,在△ABQ中求得分别求得AQ、BQ的长,结合BC知CQ的长,在△CPQ中可得PQ,根据AP=AQ+PQ得出答案.
解答 解:如图,过点A作AP⊥CD于点P,交BC于点Q,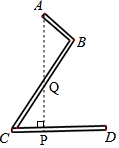
∵∠CQP=∠AQB,∠CPQ=∠B=90°,
∴∠A=∠C=50°,
在△ABQ中,∵AQ=$\frac{AB}{cosA}$=$\frac{20}{cos50°}$≈31.10,BQ=ABtanA=20tan50°≈23.84,
∴CQ=BC-BQ=60-23.84=36.16,
在△CPQ中,∵PQ=CQsinC=36.16sin50°≈27.70,
∴AP=AQ+PQ=27.70+31.10≈58.8,
答:工件如图摆放时的高度约为58.8cm.
点评 本题主要考查解直角三角形的应用,熟练掌握三角函数的定义求得相关线段的长度是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某车站在春运期间为改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到购到车票所用的时间t(以下简称购票用时,单位为分钟).下面是这次调查统计分析得到的频率分布表和频率分布直方图.解答下列问题:
某车站在春运期间为改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到购到车票所用的时间t(以下简称购票用时,单位为分钟).下面是这次调查统计分析得到的频率分布表和频率分布直方图.解答下列问题:| 分 组 | 频数 | 频率 | |
| 一组 | 0≤t<5 | 0 | 0 |
| 二组 | 5≤t<10 | 10 | 0.10 |
| 三组 | 10≤t<15 | 10 | 0.10 |
| 四组 | 15≤t<20 | 50 | 0.50 |
| 五组 | 20≤t<25 | 30 | 0.30 |
| 合 计 | 100 | 1 | |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知一次函数y=mx+n-3的图象如图,则m、n的取值范围是( )
已知一次函数y=mx+n-3的图象如图,则m、n的取值范围是( )| A. | m>0,n<3 | B. | m<0,n>3 | C. | m<0,n<3 | D. | m>0,n>3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有一直经为$\sqrt{2}$cm圆形纸片,从中剪出一个圆心角是90°的最大扇形ABC(如图所示).
有一直经为$\sqrt{2}$cm圆形纸片,从中剪出一个圆心角是90°的最大扇形ABC(如图所示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
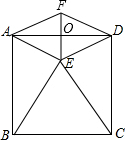 如图,正方形ABCD的边长为2,以BC为边向正方形内作等边△BCE,连接AE、DE.
如图,正方形ABCD的边长为2,以BC为边向正方形内作等边△BCE,连接AE、DE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com